Kumpulan Rumus Matematika Lengkap Dan Penjelasannya – Matematika merupakan salah satu mata pelajaran yang selalu berkaitan dengan rumus. Rumus-rumus matematika biasanya diajarkan mulai dari yang mudah hingga tersulit. Nah, pada artikel ini akan diberikan informasi mengenai kumpulan rumus matematika lengkap yang disertai dengan contoh dan penjelasannya.
Banyak yang menganggap pembelajaran matematika itu sulit. Padahal sebenarnya tidak begitu, karena setiap persoalan pada matematika dapat dikerjakan dengan kumpulan rumus matematika yang ada. Untuk itu, penting bagi setiap siswa untuk memahami rumus-rumus dasar matematika.
Nah, untuk memudahkan dalam memahami materi matematika, berikut telah dirangkum kumpulan rumus matematika lengkap beserta penjelasannya. Silahkan disimak dan dipelajari dengan baik.
Rumus Matematika Operasi Bilangan Bulat
Dalam perhitungan bilangan bulat, terdapat beberapa rumus yang perlu diketahui, diantaranya yaitu sebagai berikut:
1. Sifat Komutatif Penjumlahan
Rumus: a + b = b + a
Contoh: 2 + 5 = 5 + 2
2. Sifat Komutatif Perkalian
Rumus: a x b = b x a
Contoh: 3 x 5 = 5 x 3
3. Sifat Asosiatif Penjumlahan
Rumus: (a + b) + c = a + (b + c)
Contoh: (3 + 5) + 6 = 3 + (5 + 6)
4. Sifat Asosiatif Perkalian
Rumus: (a x b) x c = a x (b x c)
Contoh: (3 x 5) x 2 = 3 x (5 x 2)
5. Sifat Distributif Perkalian Terhadap Penjumlahan
Rumus: a x (b + c) = (a x b) + (a x c)
Contoh: 2 x (5 + 10) = (2 x 5) + (2 x 10)
6. Sifat Distributif Perkalian Terhadap Pengurangan
Rumus: a x (b – c) = (a x b) – (a x c)
Contoh: 2 x (10 – 5) = (2 x 10) – (2 x 5)
Rumus Operasi Hitung Bilangan Bulat Positif Dan Negatif
1. Rumus Penjumlahan Bilangan Bulat
a. (+) + (+) = (+)
Contoh:
3 + 5 = 8
b. (-) + (-) = (-)
Contoh:
(-2) + (-3) = (-5)
c. (+) + (-) = bisa (+) bisa juga (-)
Jika (+) lebih besar maka hasilnya (+)
Jika (-) lbh besar maka hasilnya (-)
Contoh:
8 + (-5) = 3
8 + (-10) = (-2)
d. (-) + (+) = bisa (+) bisa juga (-)
Jika (+) lebih besar maka hasilnya (+)
Jika (-) lebih besar maka hasilnya (-)
Contoh:
(-5) + 9 = 4
(-5) + 2 = (-3)
2. Rumus Pengurangan Bilangan Bulat
a. (+) – (+) = bisa (+) bisa juga (-)
Jika bilangan pertama lebih besar maka hasilnya (+)
Jika bilangan kedua lebih besar maka hasilnya (-)
Contoh:
5 – 2 = 3
5 – 9 = (-4)
b. (-) – (-) = bisa (+) bisa juga (-)
Jika bilangan pertama lebih besar maka hasilnya (+)
Jika bilangan kedua yang lebih besar maka hasilnya (-)
Contoh:
(-2) – (-5) = (-2) + 5 = 3
(-6) – (-2) = (-6) + 2 = (-4)
c. (+) – (-) = (+)
Contoh:
1 – (-5) = 1 + 5 = 6
d. (-) – (+) = (-)
Contoh:
(-2) – 5 = (-7)
3. Rumus Perkalian Bilangan Bulat
a. (+) x (+) = (+)
Contoh:
2 x 5 = 10
b. (-) x (-) = (+)
Contoh:
(-2) x (-5) = 10
c. (+) x (-) = (-)
Contoh:
2 x (-5) = (-10)
d. (-) x (+) = (-)
Contoh:
(-2) x 5 = (-10)
4. Rumus Pembagian Bilangan Bulat
a. (+) : (+) = (+)
Contoh:
10 : 5 = 2
b. (-) : (-) = (+)
Contoh:
(-10) : (-5) = 2
c. (+) : (-) = (-)
Contoh:
10 : (-5) = (-2)
d. (-) : (+) = (-)
Contoh:
(-10) : 5 = (-2)
Rumus Matematika Operasi Hitungan Campuran
Operasi hitung campuran adalah operasi hitung yang didalamnya melibatkan penjumlahan, pengurangan, perkalian, dan pembagian. Rumus atau aturan yang berlaku pada operasi hitung campuran adalah sebagai berikut:
- Penjumlahan dan pengurangan adalah setara, jadi dikerjakan mulai dari kiri
- Perkalian dan pembagian adalah setara, jadi dikerjakan mulai dari kiri
- Jika terdapat tanda kurung (), kerjakan yang ada di dalam tanda kurung terlebih dahulu
- Jika tidak ada tanda kurung (), kerjakan perkalian dan pembagian terlebih dahulu. Kemudian, kerjakan penjumlahan dan pengurangan
Contoh:
200 – 40 x 10 : 4 – (20 + 30)
= 200 – 40 x 10 : 4 – 50
= 200 – 400 : 4 – 50
= 200 – 100 – 50
= 50
Perpangkatan Dan Akar
1. Perpangkatan
Perpangkatan adalah perkalian bilangan yang sama dengan bilangan itu sendiri sebanyak jumlah pangkatnya
Contoh:
2² = 2 x 2 = 4
4² = 4 x 4 = 16
5² = 5 x 5 = 25
2. Akar
Akar adalah hasil dari suatu perpangkatan
Contoh:
√25 = 5
√16 = 6
√9 = 3
Akar Pangkat 3 Bilangan Kubik
1³ dibaca satu pangkat tiga = 1 x 1 x 1 = 1
2³ dibaca dua pangkat tiga = 2 x 2 x 2 = 8
3³ dibaca tiga pangkat tiga = 3 x 3 x 3 = 27
4³ dibaca empat pangkat tiga = 4 x 4 x 4 = 64
5³ dibaca lima pangkat tiga = 5 x 5 x 5 = 125
1, 8, 27, 64, 125, dan seterusnya adalah bilangan kubik atau bilangan pangkat 3
1. Penjumlahan Bilangan Berpangkat
Contoh:
2³ + 3³
= (2 x 2 x 2) + (3 x 3 x 3)
= 8 + 27
= 35
2. Pengurangan Bilangan Berpangkat
Contoh:
6³ – 4³
= (6 x 6 x 6) – (4 x 4 x 4)
= 216 – 64
= 152
3. Perkalian Bilangan Berpangkat
Contoh:
2³ x 4³
= (2 x 2 x 2) x (4 x 4 x 4)
= 8 x 64
= 512
4. Pembagian Bilangan Berpangkat
Contoh:
6³ : 2³
= (6 x 6 x 6) : (2 x 2 x 2)
= 216 : 8
= 27
Rumus Matematika Menentukan KPK Dan FPB
1. Rumus Mencari KPK (Kelipatan Persekutuan Terkecil)
- Tentukan faktorisasi prima dari masing-masing bilangan
- Kalikan semua faktor, jika ada faktor yg sama pilih pangkat yang tertinggi
Contoh:
12 = 2² x 3
15 = 3 x 5
Terdapat faktor yang sama yaitu 3, jadi kita ambil salah satunya saja
Jadi, KPK dari 12 dan 15 adalah 2² x 3 x 5 = 60
2. Rumus Mencari FPB (Faktor Persekutuan Terbesar)
- Tentukan faktorisasi prima dari masing-masing bilangan
- Mengalikan faktor yang sama yang memiliki pangkat terkecil
Contoh:
27 = 3³
18 = 2 x 3²
Terdapat faktor yang sama yaitu 3, dan yang memiliki pangkat terkecil adalah 3²
Jadi, FPB dari 27 dan 18 adalah 3² = 9
Kumpulan Rumus Matematika Mengubah Pecahan
1. Mengubah Pecahan Biasa ke Bentuk Persen
Untuk mengubah pecahan ke bentuk persen dapat dilakukan dengan mengubah penyebut pecahan ke bentuk 100
Contoh:
1/4 = 25/100 = 25%
1/2 = 50/100 = 50%
2. Mengubah Bentuk Persen ke Pecahan Biasa
Untuk mengubah bentuk persen ke pecahan dapat dilakukan dengan menambahkan penyebut 100 pada bilangan persen
Contoh:
50% = 50/100 = 1/2
20% = 20/100 = 1/5
3. Mengubah Desimal menjadi Pecahan Biasa
Untuk mengubah pecahan desimal ke pecahan biasa dapat dilakaukan dengan melihat tanda koma pada desimal:
- Jika satu angka dibelakang koma maka diubah menjadi pecahan persepuluh
- Jika dua angka dibelakang koma maka diubah menjadi pecahan perseratus
- Jika tiga angka dibelakang koma maka diubah menjadi pecahan perseribu, dan seterusnya
Contoh:
0,5 = 5/10 = 1/2
0,25 = 25/100 = 1/4
0,125 = 125/1000 = 1/8
4. Mengubah Pecahan Biasa menjadi Desimal
Untuk mengubah pecahan biasa ke desimal dapat dilakaukan dengan mengubah penyebut pecahan menjadi 10, 100, 1000, dan seterusnya.
Contoh:
1/5 = 2/10 = 0,2
1/25 = 4/100 = 0,04
1/8 = 125/1000 = 0,125
Kumpulan Rumus Matematika Operasi Hitung Pecahan
1. Rumus Penjumlahan Pecahan
a. Penjumlahan Pecahan Berpenyebut Sama
a/b + c/b = (a + c)/b
Contoh:
1/4 + 2/4 = (1 + 2)/4 = 3/4
2/6 + 3/6 = (2 + 3)/6 = 5/6
b. Penjumlahan Pecahan Beda Penyebut
a/b + c/d = (a x d) + (b x c)/(b x d)
Contoh:
1/2 + 1/3 = (1 x 3) + (2 x 1)/(2 x 3) = (3 + 2)/ 6 = 5/6
2/3 + 1/5 = (2 x 5) + (3 x 1)/(3 x 5) = (10 + 3)/ 15 = 13/15
2. Rumus Pengurangan Pecahan
a. Pengurangan Pecahan Berpenyebut Sama
a/b – c/b = (a – c)/b
Contoh:
3/4 – 2/4 = (3 – 2)/4 = 1/4
5/6 – 3/6 = (5 – 3)/6 = 2/6 = 1/3
b. Pengurangan Pecahan Beda Penyebut
a/b – c/d = (a x d) – (b x c)/(b x d)
Contoh:
1/2 – 1/3 = (1 x 3) – (2 x 1)/(2 x 3) = (3 – 2)/ 6 = 1/6
2/3 – 1/5 = (2 x 5) – (3 x 1)/(3 x 5) = (10 – 3)/ 15 = 7/15
3. Rumus Perkalian Pecahan
a/b x c/d = (a x c)/(b x d)
Contoh:
1/2 x 1/3 = (1 x 1)/(2 x 3) = 1/6
3/4 x 2/5 = (3 x 2)/(4 x 5) = 6/20 = 3/10
4. Rumus Pembagian Pecahan
a/b : c/d = a/b x d/c
Contoh:
1/8 : 1/4 = 1/8 x 4/1 = (1 x 4)/(8 x 1) = 4/8 = 1/2
1/2 : 1/4 = 1/2 x 4/1 = (1 x 4)/(2 x 1) = 4/2 = 2
Rumus Matematika Hubungan Antar Satuan
1. Satuan Panjang
- 1 km = 10 hm
- 1 km = 100 dam
- 1 km = 1.000 m
- 1 km = 10.000 dm
- 1 km = 100.000 cm
- 1 km = 1.000.000 mm
2. Satuan Berat
- 1 kg = 10 hg
- 1 kg = 100 dag
- 1 kg = 1.000 g
- 1 kg = 10.000 dg
- 1 kg = 100.000 cg
- 1 kg = 1.000.000 mg
- 1 ton = 1.000 kg
- 1 ton = 10 kuintal
- 1 kuintal = 100 kg
- 1 kg = 10 ons
3. Satuan Volume Dalam Kubik
- 1 km³ = 1.000 hm³
- 1 km³ = 1.000.000 dam³
- 1 km³ = 1.000.000.000 m³
- 1 km³ = 1.000.000.000.000 dm³
- 1 km³ = 1.000.000.000.000.000 cm³
- 1 km³ = 1.000.000.000.000.000.000 mm³
4. Satuan Volume Dalan Liter
- 1 kl = 10 hl
- 1 kl = 100 dal
- 1 kl = 1.000 l
- 1 kl = 10.000 dl
- 1 kl = 100.000 cl
- 1 kl = 1.000.000 ml
- 1 dm³ = 1 liter
- 1 cm³ = 1 ml
5. Satuan Waktu
- 1 Menit = 60 Detik
- 1 Jam = 60 Menit
- 1 Hari = 24 Jam
- 1 Minggu = 7 Hari
- 1 Bulan = 30 / 31 Hari
- 1 Bulan = 4 Minggu
- 1 Tahun = 12 Bulan
- 1 Tahun = 52 Minggu
- 1 Windu = 8 Tahun
- 1 Dekade = 10 Tahun
- 1 Dasawarsa = 10 Tahun
- 1 Abad = 100 Tahun
- 1 Milenium = 1.000 Tahun
6. Konversi Satuan Detik
- 1 menit = 60 detik
- 1 jam = 3.600
- 1 hari = 86400
- 1 bulan = 2.592.000 detik
- 1 tahun = 31.104.000 detik
Kumpulan Rumus Matematika Lengkap Menghitung Luas Bangun Datar
| Nama Bangun Datar | Rumus Luas |
| Persegi | s x s Keterangan: s = sisi persegi |
| Persegi Panjang | p x l Keterangan: p = panjang l = lebar |
| Segitiga | 1/2 x a x t Keterangan: a = alas t = tinggi |
| Trapesium | 1/2 x (a + b) x t keterangan: a, b = sisi sejajar t = tinggi |
| Jajar Genjang | a x t Keterangan: a = alas t = tinggi |
| Belah Ketupat | 1/2 x d1 x d2 Keterangan: d1 = diagonal 1 d2 = diagonal 2 |
| Layang-Layang | 1/2 x d1 x d2 Keterangan: d1 = diagonal 1 d2 = diagonal 2 |
| Lingkaran | π x r² Keterangan: π = 22/7 atau 3,14 r = jari-jari |
Kumpulan Rumus Matematika Lengkap Menghitung Keliling Bangun Datar
| Nama Bangun Datar | Rumus Keliling |
| Persegi | 4 x s Keterangan: s = sisi persegi |
| Persegi Panjang | 2 x (p + l) Keterangan: p = panjang l = lebar |
| Segitiga | s + s + s Keterangan: s = sisi segitiga |
| Trapesium | s + s + s + s Keterangan: s = sisi trapesium |
| Jajar Genjang | 2 x (a + b) Keterangan: a, b = sisi sejajar |
| Belah Ketupat | 4 x s Keterangan: s = sisi belah ketupat |
| Layang-Layang | s + s + s + s Keterangan: s = sisi layang-layang |
| Lingkaran | 2 x π x r Keterangan: π = 22/7 atau 3,14 r = jari-jari lingkaran |
Kumpulan Rumus Matematika Menghitung Volume Bangun Ruang
| Kubus | V = s x s x s Keterangan: s = rusuk kubus |
| Balok | V = p x l x t Keterangan: p = panjang l = lebar t = tinggi |
| Limas | V = 1/3 x Luas Alas x Tinggi Keterangan: Luas alas tergantung bentuk sisi alasnya |
| Prisma | V = Luas Alas x Tinggi Keterangan: Luas alas tergantung bentuk sisi alasnya |
| Kerucut | V = 1/3 x π x r² x t Keterangan: π = 22/7 atau 3,14 r = jari-jari kerucut t = tinggi kerucut |
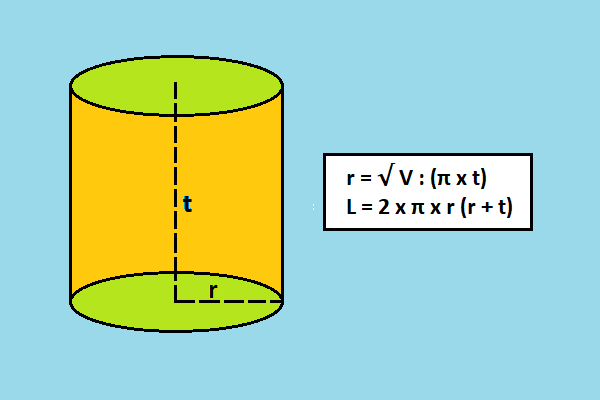
| Tabung | V = π x r² x t Keterangan: π = 22/7 atau 3,14 r = jari-jari tabung t = tinggi tabung |
| Bola | V = 4/3 x π x r³ Keterangan: π = 22/7 atau 3,14 r = jari-jari bola |
Kumpulan Rumus Matematika Menghitung Luas Permukaan Bangun Ruang
| Kubus | L = 6 x s x s Keterangan: s = rusuk kubus |
| Balok | L = 2 (p x l + p x t + l x t) Keterangan: p = panjang l = lebar t = tinggi |
| Limas | L = luas alas + luas seluruh sisi tegak Keterangan: Luas alas tergantung bentuk sisi alasnya, Luas sisi tegak limas berbentuk segitiga |
| Prisma | L = (2 x luas alas) + (keliling alas x tinggi) Keterangan: Luas alas tergantung bentuk sisi alasnya |
| Kerucut | L = π x r (r + s) Keterangan: π = 22/7 atau 3,14 r = jari-jari kerucut s = garis pelukis kerucut |
| Tabung | L = 2 x π x r x (r + t) Keterangan: π = 22/7 atau 3,14 r = jari-jari tabung t = tinggi tabung |
| Bola | L = 4 x π x r² Keterangan: π = 22/7 atau 3,14 r = jari-jari bola |
Mengenal Sifat-Sifat Bangun Datar
1. Sifat-Sifat Persegi
- Memiliki 4 sisi sama panjang
- Memiliki 4 titik sudut
- Memiliki 4 sudut siku-siku
- Memiliki 2 diagonal sama panjang
2. Sifat-Sifat Persegi Panjang
- Memiliki 4 buah sisi
- Memiliki 2 pasang sisi sama panjang
- Memiliki 4 titik sudut
- Memiliki 4 sudut siku-siku
- Mempunyai 2 diagonal sama panjang
3. Sifat-Sifat Segitiga Sama Kaki
- Memiliki 3 buah sisi
- Memiliki 3 titik sudut
- Memiliki 2 sisi sama panjang
- Memiliki 2 sudut sama besar
4. Sifat-Sifat Segitiga Sama Sisi
- Memiliki 3 buah sisi sama panjang
- Memiliki 3 titik sudut
- Memiliki 3 sudut sama besar (60º)
5. Sifat-Sifat Segitiga Siku-Siku
- Memiliki 3 buah sisi
- Memiliki 3 titik sudut
- Memiliki 1 buah sudut siku-siku 45º
6. Sifat-Sifat Segitiga Lancip
- Memiliki 3 buah sisi
- Memiliki 3 titik sudut
- Memiliki 3 sudut yang besarnya kurang dari 90º
7. Sifat-sifat Segitiga Tumpul
- Memiliki 3 buah sisi
- Memiliki 3 titik sudut
- Memiliki 1 sudut yang besarnnya lebih dari 90º dan kurang dari 180º
8. Sifat-Sifat Segitiga Sembarang
- Memiliki 3 buah sisi yang panjang berbeda
- Memiliki 3 titik sudut yang besarnya berbeda
- Jumlah ketiga sudutnya 180º
9. Sifat-Sifat Jajar Genjang
- Memiliki 4 buah sisi
- Memiliki 4 titik sudut
- Sisi-sisi yang berhadapan sejajar dan sama panjang
- Sudut-sudut yang berhadapan sama besar
- Memiiki 2 diagonal yang saling membagi dua sama panjang
10. Sifat-Sifat Trapesium Sama Kaki
- Memiliki 4 buah sisi
- Memiliki 4 titik sudut
- Memiliki sepasang sisi sejajar yang beda panjang
- Memiliki 2 sisi yang sama panjang
- Memiliki 2 pasang sudut yang besarnya sama
11. Sifat-Sifat Trapesium Siku-Siku
- Memiliki 4 buah sisi
- Memiliki 4 titik sudut
- Memiliki sepasang sisi sejajar yang beda panjang
- Memiliki 2 sudut siku-siku
12. Sifat-Sifat Trapesium Sembarang
- Memiliki 4 buah sisi yang panjang berbeda
- Memiliki 4 titik sudut
- Memiliki sepasang sisi sejajar yang beda panjang
13. Sifat-Sifat Layang-layang
- Memiliki 4 buah sisi
- Memiliki 4 titik sudut
- Memiliki 2 pasang sisi sama panjang
- Memiliki sepasang sudut sama besar
- Memiliki 2 diagonal berpotongan tegak lurus
14. Sifat-Sifat Belah Ketupat
- Memiliki 4 buah sisi sama panjang
- Memiliki 4 titik sudut
- Memiliki 2 pasang sudut sama besar
- Memiliki 2 diagonal berpotongan tegak lurus
15. Sifat-Sifat Lingkaran
- Memiliki 1 buah sisi
- Tidak memiliki titik sudut
- Memiliki 1 titik pusat
- Memiliki jari-jari
- Memiliki diameter
Mengenal Sifat-Sifat Bangun Ruang
1. Sifat-Sifat Kubus
- Memiliki 6 sisi berbentuk persegi
- Memiliki 12 rusuk sama panjang
- Memiliki 8 titik sudut
2. Sifat-Sifat Balok
- Memiliki 6 sisi berbentuk persegi dan persegi panjang
- Memiliki 12 rusuk, terdiri dari 4 rusuk panjang, 4 rusuk lebar, 4 rusuk tinggi
- Memiliki 8 titik sudut
3. Sifat-Sifat Prisma Segitiga
- Memilik 5 buah sisi
- Memiliki 9 buah rusuk
- Memiliki 6 buah titik sudut
- Sisi alas dan atap berbentuk segitiga
4. Sifat-Sifat Prisma Segiempat
- Memilik 6 buah sisi
- Memiliki 12 buah rusuk
- Memiliki 8 buah titik sudut
- Sisi alas dan atap berbentuk segiempat
5. Sifat-Sifat Limas Segitiga
- Memiliki 4 buah sisi
- Memiliki 6 buah rusuk
- Memiliki 4 buat titik sudut
- Sisi alas berbentuk segitiga
6. Sifat-Sifat Limas Segiempat
- Memiliki 5 buah sisi
- Memiliki 8 buah rusuk
- Memiliki 5 buat titik sudut
- Sisi alas berbentuk segiempat
7. Sifat-Sifat Kerucut
- Memiliki 2 buah sisi
- Memiliki 1 buah rusuk
- Memiliki 1 buah titik sudut
- Sisi alas berbentuk lingkaran
8. Sifat-Sifat Tabung
- Memiliki 3 buah sisi
- Memiliki 2 buah rusuk
- Tidak memiliki titik sudut
- Sisi alas dan atas berbentuk lingkaran
9. Sifat-Sifat Bola
- Memiliki 1 buah sisi
- Tidak memiliki rusuk
- Tidak memiliki titik sudut
- Memiliki titik pusat
Kumpulan Jumlah Simetri Lipat dan Simetri Putar Bangun Datar
| Nama Bangun | Simetri Lipat | Simetri Putar |
| Persegi | 4 | 4 |
| Persegi Panjang | 2 | 2 |
| Segitiga Sama Kaki | 1 | – |
| Segitiga Sama Sisi | 3 | 3 |
| Jajar Genjang | – | 2 |
| Trapesium Sama Kaki | 1 | – |
| Layang-layang | 1 | – |
| Belah Ketupat | 2 | 2 |
| Lingkaran | tak terhingga | tak terhingga |
| Elips | 2 | 2 |
| Segi Lima Beraturan | 5 | 5 |
| Segi Enam Beraturan | 6 | 6 |
| Sgi Delapan Beraturan | 8 | 8 |
Rumus Matematika Jarak Dan Kecepatan
Jarak = kecepatan x jarak
Kecepatan = jarak : waktu
Waktu = jarak : kecepatan
Rumus Matematika Menentukan Skala
Rumus Skala = Jarak Pada Peta : Jarak Sebenarnya
Rumus Jarak Pada Peta = Jarak Sebenarnya x Skala
Rumus Jarak Sebenarnya = Jarak Pada Peta : Skala
Mengukur Besar Sudut
Mengukur sudut dapat dilakukan dengan busur derajat. Berikut merupakan nama jenis-jenis sudut berdasarkan nilainya:
- Sudut lancip adalah sudut yang kurang dari 90º
- Sudut tumpul adalah sudut yang lebih dari 90 derajat dan kurang dari 180º
- Sudut siku-siku adalah sudut yang besarnya 90º
- Sudut lurus adalah sudut yang besarnya 180º
- Sudut refleks adalah sudut yang lebih dari 180º dan kurang dari 360º
Penyajian Dan Pengolahan Data
- Nilai minimum adalah nilai yang terkecil dan yang terendah dari semua data
- Nilai maksimal adalah nilai yang tertinggi dari semua data yang ada didalamnya
- Modus adalah nilai yang paling banyak muncul
- Median adalah nilai tengah
- Mean (rata-rata) adalah jumlah nilai data dibagi dengan banyaknya data. Rumusnya adalah menjumlahkan semua data, kemudian dibagi dengan jumlah data
Contoh:
| 7 | 8 | 6 | 9 | 8 | 8 | 7 | 9 | 6 | 10 |
| 10 | 8 | 7 | 6 | 7 | 9 | 6 | 10 | 8 | 9 |
Nilai maksimum = 10
Nilai minimum = 6
Mean/rata-rata = (6 x 4) + (7 x 4) + (8 x 5) + (9 x 4) + (10 x 3) : 20 = 7,9
Median = 8
Modus = 8
Sistem Koordinat
- Sumbu x juga disebut dengan Absis (x) dan untuk sumbu y disebut juga dengan Ordinat (y)
- Sebuah bidang koordinat cartesius akan terbentuk oleh 2 buah sumbu yakni sumbu tegak (sumbu y) dan sumbu mendatar (sumbu x)
- Dari titik nol sumbu tegak akan ke atas dan sumbu mendatar akan ke kanan yang mempunyai nilai positif
- Dari titik nol sumbu tegak akan ke bawah dan sumbu mendatar akan ke kiri yang mempunyai nilai negatif
- Mencari titik koordinat suatu objek dapat dicari dengan mencari letak pada sumbu x ke kanan ataupun ke kiri dengan letak pada sumbu y ke atas ataupun ke bawah
Demikianlah informasi mengenai kumpulan rumus matematika lengkap dan penjelasannya. Semoga bermanfaat dalam belajar materi matematika.