Rumus Luas Permukaan Tabung Jika Diketahui Volumenya – Tabung merupakan salah satu bangun ruang yang memiliki volume dan luas permukaan. Pada kesempatan kali ini akan dibahas tentang rumus yang digunakan untuk mencari luas permukaan tabung jika telah diketahui volumenya.
Untuk menetukan luas permukaan tabung yang telah diketahui volumenya, rumusnya adalah mencari panjang jari-jarinya terlebih dahulu. Jika jari-jari tabung telah diketahui, barulah menghitung luas permukaannya dengan menggunakan ukuran jari-jari tabung.
Nah, bagi yang ingin mengetahui bagaimana langkah-langkah mencari luas permukaan tabung yang telah diketahui volumenya, maka silahkan simak pembahasan berikut ini mengenai cara menghitung luas permukaan tabung jika telah diketahui volumenya.
Rumus Luas Permukaan Tabung Jika Diketahui Volumenya
Untuk menghitung luas permukaan sebuah tabung dari volumenya, maka kita harus mengetahui bagaimana cara menghitung volume tabung. Rumus volume tabung adalah V = π x r² x t.
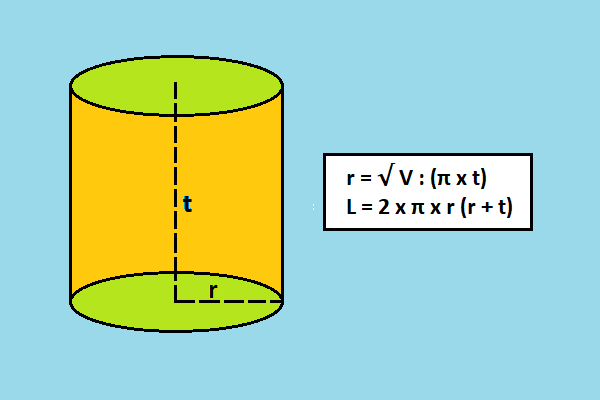
Dari rumus volume tersebut, ukuran jari-jari tabung dapat ditentukan dengan rumus r = √ V : (π x t). Setelah jari-jari ditemukan, kemudian menghitung luas permukaan tabung. Jadi, langkah-langkah mennghitung luas permukaan tabung jika volumenya telah diketahui adalah:
- Mencari jari-jari tabung dengan rumus r = √ V : (π x t)
- Menghitung luas permukaan tabung dengan rumus L = 2 x π x r (r + t)
Contoh Soal
1. Berapakah luas permukaan tabung yang memiliki volume 1.540 cm³ dan tinggi 10 cm?
Penyelesaian:
r = √ V : (π x t)
r = √ 1.540 : (22/7 x 10)
r = √ 1.540 : 220/7
r = √ 49
r = 7 cm
L = 2 x π x r (r + t)
L = 2 x 22/7 x 7 (7 + 10)
L = 44 x 17
L = 748 cm²
Jadi, luas permukaan tabung dari volume 1.540 cm³ dan tinggi 10 cm adalah 748 cm².
2. Sebuah tabung memiliki volume 785 cm³. Jika tinggi tabung 10 cm, berapa luas permukaannya?
Penyelesaian:
r = √ V : (π x t)
r = √ 785 : (3,14 x 10)
r = √ 785 : 31,4
r = √ 25
r = 5 cm
L = 2 x π x r (r + t)
L = 2 x 3,14 x 5 (5 + 10)
L = 31,4 x 15
L = 471 cm²
Jadi, luas permukaan tabung dari volume 785 cm³ dan tinggi 10 cm adalah 471 cm².
Demikianlah pembahasan mengenai cara menghitung luas permukaan tabung jika telah diketahui volumenya beserta contoh soal pembahasannya. Semoga bermanfaat.
Baca Lagi :