Operasi Penjumlahan Dan Pengurangan Bilangan Bulat – Bilangan bulat merupakan konsep dasar yang digunakan untuk melakukan operasi perhitungan, seperti penjumlahan dan pengurangan. Nah, pada kesempatan kali ini akan dijelaskan rumus yang digunakan untuk menghitung operasi penjumlahan dan pengurangan pada bilangan bulat.
Bilangan bulat itu sendiri merupakan bilangan matematika yang terdiri dari bilangan negatif, nol dan bilangan positif. Bilangan bulat disimbolkan dengan z (zahlen ; bilangan) yang berasal dari bahasa Jerman. Jika dinotasikan dengan angka, maka himpunan bilangan bulat dituliskan { . . ., -4, -3, -2, -1, 0, 1, 2, 3, 4}.
Dalam melakukan operasi penjumlahan dan pengurangan pada bilangan bulat, kita harus mengetahui sifat-sifat penjumlahan dan pengurangan yang berlaku pada bilangan bulat. Nah, bagi yang belum tahu apa saja sifat penjumlahan dan pengurangan bilangan bulat, simak pembahasan berikut ini.
Sifat Penjumlahan Dan Pengurangan Bilangan Bulat
A. Sifat Penjumlahan Bilangan Bulat
Operasi penjumlahan pada bilangan bulat memiliki beberapa sifat yang perlu kita ketahui. Jika kita melihat garis bilangan, maka bilangan bulat yang dijumlahkan dengan suatu bilangan bulat positif akan bergerak ke arah kanan dan nilainya pun menjadi semakin besar. Adapun sifat-sifat operasi penjumlahan pada bilangan bulat, yaitu sebagai berikut:
- Sifat Komutatif
Sifat komutatif adalah sifat pertukaran yang berlaku pada bilangan bulat. Secara umum, sifat komutatif dituliskan dengan rumus a + b = b + a. Contoh sifat komutatif pada operasi penjumlahan bilangan bulat yaitu 5 + 3 = 3 + 5 = 8.
- Sifat Asosiatif
Sifat asosiatif pada penjumlahan bilangan bulat merupakan sifat pengelompokan. Secara umum, sifat asosiatif dituliskan dengan rumus (a + b) + c = a + (b + c). Contoh sifat asosiatif pada operasi penjumlahan bilangan bulat yaitu (4 + 1) + 2 = 4 + (1+ 2) = 7.
- Sifat Identitas
Unsur identitas pada operasi penjumlahan bilangan bulat adalah bilangan 0. Angka 0 dikatakan sebagai unsur identitas karena jika kita menjumlahkan bilangan bulat dengan angka 0, maka hasil akan tetap. Secara umum, unsur identitas pada bilangan bulat dituliskan dengan rumus 0 + a = a + 0. Contoh unsur identitas pada operasi penjumlahan bilangan bulat yaitu 5 + 0 = 0 + 5 = 5.
- Unsur Invers
Unsur inverts adalah unsur lawan. Dimana a adalah lawan -a, dan -a adalah lawan a. Secara umum, sifat invers ini dituliskan dengan a + (-a) = 0. Contoh unsur invers pada operasi pengurangan bilangan bulat yaitu 3 + (-3) = 0.
- Sifat Tertutup
Operasi penjumlahan pada bilangan bulat juga berlaku sifat tertutup, dimana penjumlahan bilangan bulat akan menghasilkan bilangan bulat juga. Misalnya a dan b adalah bilangan, maka a + b = c, dimana c merupakan bilangan bulat. Contoh sifat tertutup pada bilangan bulat yaitu 3 + 5 = 8 , dimana 3, 5, dan 8 adalah bilangan bulat.
B. Sifat Pengurangan Bilangan Bulat
Dalam garis bilangan, suatu bilangan bulat yang dikurangi dengan suatu bilangan bulat positif akan bergerak ke arah kiri dan nilainya menjadi semakin kecil. Adapun sifat-sifat dalam operasi pengurangan bilangan bulat, yaitu sebagai berikut:
- a – b = a + (-b)
- a – (-b) = a + b
Contoh:
5 – 2 = 5 + (-2) = 3
4 – (-2) = 4 + 2 = 6
- Sifat komutatif dan asosiatif tidak berlaku pada operasi pengurangan bilangan bulat
a – b ≠ b – a
(a – b) – c ≠ a – (b – c)
Contoh:
5 – 2 ≠ 2 – 5
(4 – 2) – 1 ≠ 4 – (2 – 1)
- Operasi pengurangan bilangan bulat yang melibatkan bilangan 0
a – 0 = a
0 – a = -a
Contoh:
3 – 0 = 3
0 – 2 = -2
- Sifat Tertutup Pada Operasi Pengurangan Bilangan Bulat
Operasi pengurangan pada bilangan bulat yang melibatkan dua bilangan bulat, maka hasil operasinya juga merupakan bilangan bulat. Misalnya a dan b merupakan bilangan bulat, maka a – b = c, dimana c merupakan bilangan bulat. Contoh sifat tertutup operasi pengurangan bilangan bulat yaitu 3 – 1 = 2 di mana 2, 1, dan 2 adalah bilangan bulat.
Operasi Penjumlahan Dan Pengurangan Bilangan Bulat
Untuk menghitung operasi penjumlahan dan pengurangan pada bilangan bulat, cara yang paling mudah yaitu menggunakan garis bilangan. Garis bilangan itu sendiri merupakan garis lurus dengan titik-titik yang diasumsikan sebagai suatu bilangan real yang berututan.
A. Operasi Penjumlahan Bilangan Bulat
Untuk memudahkan dalam memahami operasi penjumlahan pada bilangan bulat, berikut akan dijelaskan langsung melalui contoh soal dan cara penyelesaiannya dengan menggunakan garis bilangan. Silahkan perhatikan dengan baik ya.
Contoh Soal
2 + 3 = …?
Penyelesaian:
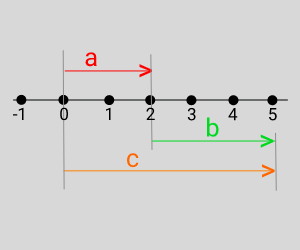
- Langkah pertama adalah membuat garis bilangan
- Buatlah garis a : Tarik garis dari angka nol sepanjang 2 satuan
- Buatlah garis b : Tarik garis dari akhir garis a ke kanan sepanjang 3 satuan
- Buatlah garis c : Tarik garis dari angka nol hingga akhir garis b
- Hasil penjumlahan ditunjukkan oleh garis c, yakni 2 + 3 = 5
B. Operasi Pengurangan Bilangan Bulat
Seperti penjelasan di atas, untuk memudahkan dalam memahami operasi pengurangan pada bilangan bulat, berikut akan dijelaskan langsung melalui contoh soal beserta cara penyelesaiannya dengan menggunakan garis bilangan. Silahkan disimak dengan baik.
Contoh Soal
3 – 5 = …?
Penyelesaian:

- Langkah pertama adalah membuat garis bilangan
- Buat garis a : Tarik garis dari angka nol ke kanan sepanjang 3 satuan
- Buat garis b : Tarik garis ke kiri dari akhir garis a sepanjang 5 satuan
- Buat garis c : Tarik garis dari angka nol hingga akhir garis b
- Hasil pengurangan ditunjukkan oleh garis c, yakni 3 – 5 = (-2)
Demikianlah pembahasan mengenai cara menghitung operasi penjumlahan dan pengurangan pada bilangan bulat. Semoga bermanfaat.
Baca Lagi :