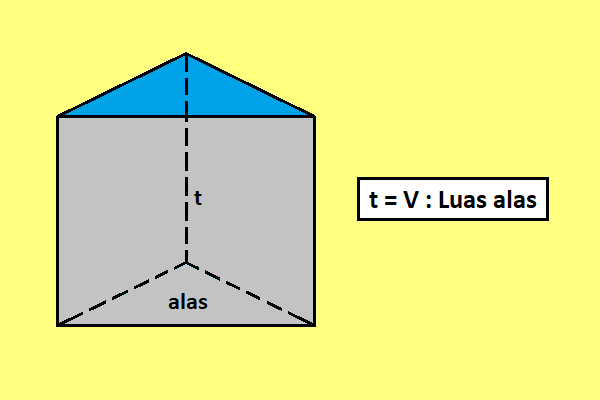
Rumus Mencari Tinggi Prisma – Prisma merupakan bangun ruang dengan sisi alas dan sisi atas berbentuk segi-n beraturan, serta beberapa sisi tegak berbentuk segi empat. Jarak antara sisi alas dan sisi atas prisma adalah tinggi prisma. Pada kesempatan kali ini akan dibahas tentang rumus mencari tinggi prisma beserta contoh soalnya.
Untuk menetukan tinggi suatu bangun ruang prisma, hal pertama yang harus diketahui adalah bentuk sisi alasnya. Sisi alas prisma memiliki berbagai macam bentuk, seperti segitiga, segi empat, segi lima, segi enam, dan seterusnya. Dengan mengetahui luas sisi alasnya, maka memudahkan mencari tinggi prisma.
Nah, bagi yang belum tahu bagaimana cara mencari tinggi prisma yang telah diketahui luas alas dan volumenya, silahkan simak pembahasan berikut ini mengenai rumus mencari tinggi prisma.
Rumus Mencari Tinggi Prisma Dan Contoh Soalnya
Untuk mencari tinggi prisma yang telah diketahui volumenya, kita perlu memahami rumus volume prisma. Volume prisma merupakan perkalian dari luas alas dan tinggi prisma (V = Luas alas x tinggi). Sehingga, tinggi prisma dapat ditentukan dengan rumus sebagai berikut:
| t = V : La |
Keterangan:
t = tinggi prisma
V = volume prisma
La = luas alas prisma
Untuk menerapkan rumus tersebut, kita juga perlu mengetahui rumus-rumus luas bangun datar pembentuk sisi alas prisma. Adapun rumus-rumusnya adalah sebagai berikut:
| Luas segitiga = 1/2 x alas x tinggi |
| Luas persegi = sisi x sisi |
| Luas persegi panjang = panjang x lebar |
| Luas belah ketupat = 1/2 x diagonal 1 x diagonal 2 |
| Luas trapesium = 1/2 x (jumlah sisi sejajar) x tinggi |
Contoh Soal
1. Sebuah prisma segitiga memiliki volume 600 cm³. Jika sisi panjang sisi alas 10 dan tinggi alasnya 8 cm, berapakah tinggi prisma segitiga?
Penyelesaian:
t = V : La
t = V : (1/2 x alas x tinggi)
t = 600 : (1/2 x 10 x 8)
t = 600 : 40
t = 15 cm
Jadi, tinggi prisma segitiga adalah 15 cm.
2. Prisma dengan sisi alas belah ketupat memiliki volume 2.880 cm³. Jika panjang diagonal belah ketupat masing-masing 16 cm dan 18 cm, berapa tinggi prisma belah ketupat?
Penyelesaian:
t = V : La
t = V : (1/2 x diagonal 1 x diagonal 2)
t = 2.880 : (1/2 x 16 x 18)
t = 2.880 : 144
t = 20 cm
Jadi, tinggi prisma belah ketupat adalah 20 cm.
3. Diketahui volume prisma trapesium adalah 2.600 cm³. Jika panjang garis sejajar trapesium masing-masing 12 cm dan 14 cm serta tinggi trapesium 8 cm, berapakah tinggi prisma trapesium?
Penyelesaian:
t = V : La
t = V : [1/2 x (jumlah sisi sejajar) x tinggi]
t = 2.600 : [1/2 x (12 + 14) x 8]
t = 2.600 : (1/2 x 26 x 8)
t = 2.600 : 104
t = 25 cm
Jadi, tinggi prisma trapesium adalah 25 cm.
Demikianlah pembahasan mengenai rumus mencari tinggi prisma beserta contoh soalnya. Semoga bermanfaat.