Rumus Pythagoras Menghitung Segitiga Siku-Siku – Apa itu rumus pythagoras? Dan bagaiaman rumus tersebut digunakan untuk menghitung sisi-sisi pada segitiga siku-siku? Nah, pada kesempatan kali ini akan dibahas tentang rumus pythagoras menghitung sisi-sisi pada segitiga siku-siku.
Rumus pytharoras merupakan ketentuan matematika yang digunakan untuk mencari ukuran sisi pada segitiga siku-siku yang belum diketahui. Rumus ini berasal dari teorema pythagoras yang berbunyi: “kuadrat sisi miring pada segitiga siku-siku sama dengan jumlah kuadrat kedua sisi lainnya”.
Segitiga siku-siku adalah segitiga yang memiliki dua sisi yang saling tegak lurus, serta sisi lainnya miring dan merupakan sisi terpanjang. Jika salah satu sisi pada segitiga siku-siku belum diketahui, maka kita dapat menghitungnya dengan rumus pythagoras. Berikut pembahasannya.
Rumus Pythagoras Menghitung Segitiga Siku-Siku
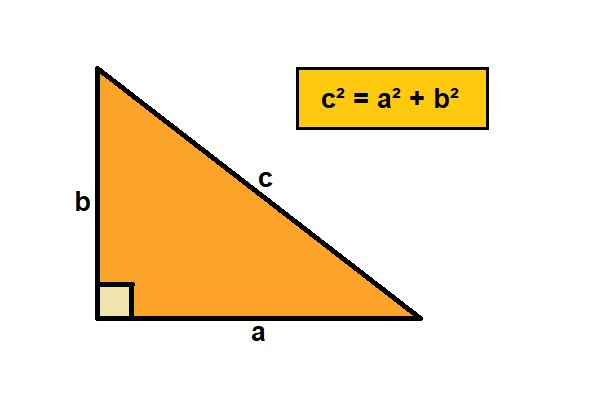
Perhatikan gambar di atas, sisi-sisi segitiga siku ditunjukan oleh a, b, dan c. Dimana sisi c merupakan sisi terpanjangnya. Dari pernyataan teorema pythagoras, maka rumus pythagoras dapat dituliskan sebagai berikut:
| c² = a² + b² |
Keterangan:
c = sisi miring
a = sisi alas
b = sisi tinggi
A. Rumus Mencari Sisi Alas Segitiga Siku-Siku
Rumus pythagoras yang digunakan untuk mencari sisi alas pada segitiga siku-siku jika telah diketahui sisi miring dan tingginya adalah sebagai berikut:
| a² = c² – b² |
| a = √(c² – b²) |
Contoh Soal
Segitiga siku-siku memiliki sisi miring 5 cm. Jika tingginya 3 cm, berapa panjang sisi alasnya?
Penyelesaian:
a = √(c² – b²)
a = √(5² – 3²)
a = √(25 – 9)
a = √16
a = 4 cm
Jadi, panjang sisi alas segitiga siku-siku adalah 4 cm.
B. Rumus Mencari Tinggi Segitiga Siku-Siku
Rumus pythagoras yang digunakan untuk mencari tinggi atau sisi tegak pada segitiga siku-siku yang telah diketahui sisi miring dan alasnya adalah sebagai berikut:
| b² = c² – a² |
| b = √(c² – a²) |
Contoh Soal
Segitiga siku-siku memiliki sisi miring 10 cm. Jika panjang sisi alasnya 8 cm, berapa tingginya?
Penyelesaian:
b = √(c² – a²)
b = √(10² – 8²)
b = √(100 – 64)
b = √36
b = 6 cm
Jadi, tinggi segitiga siku-siku adalah 6 cm.
C. Cara Mencari Sisi Miring Segitiga Siku-Siku
Untuk mencari sisi miring pada segitiga siku-siku yang telah diketahui alas dan tingginya adalah sebagai berikut:
| c² = a² + b² |
| c = √(a² + b²) |
Contoh Soal
Segitiga siku-siku memiliki sisi alas 9 cm dan tinggi 12 cm. Berapa panjang sisi miringnya?
Penyelesaian:
c = √(a² + b²)
c = √(9² – 12²)
c = √(81 – 144)
c = √225
c = 15 cm
Jadi, sisi miring segitiga siku-siku adalah 15 cm.
Demikianlah pembahasan mengenai rumus pythagoras menghitung sisi segitiga siku-siku dan contoh soalnya. Semoga bermanfaat.