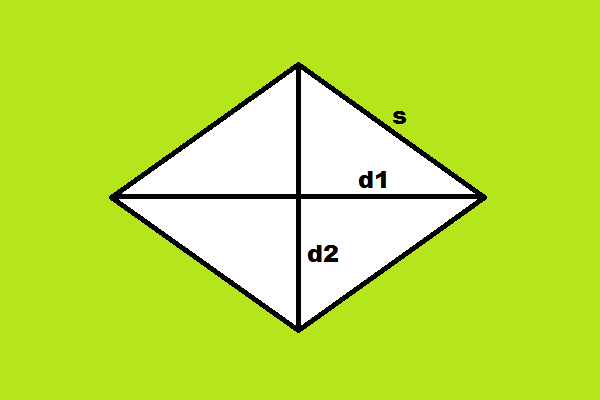
Rumus Bangun Ruang Lengkap dan Contoh Soal

Rumus Bangun Ruang Lengkap dan Contoh Soal – Bangun ruang adalah bangun tiga dimensi yang memiliki volume. Selain volume, bangun ruang juga memiliki luas permukaan. Volume dan luas permukaan tersebut dapat dihitung dengan rumus matematika. Nah, pada kesempatan kali ini akan dibahas mengenai rumus bangun ruang dan contoh soalnya.

Secara umum, volume bangun ruang adalah luas sisi alas dikali tinggi. Sedangkan luas permukaannya adalah jumlah seluruh luas sisinya. Mengingat sisi-sisi bangun ruang merupakan gabungan dari bangun datar, maka dalam menghitung bangun ruang, kita juga harus mengetahui rumus bangun datar. Berikut merupakan kumpulan rumus luas dan keliling bangun datar.

Bangun Datar	Rumus Luas	Rumus Keliling
Persegi	s × s	4 × s
Persegi Panjang	p × l	2 × (p + l)
Segitiga	1/2 × a × t	s + s + s
Trapesium	1/2 × (a + b) × t	s + s + s + s
Jajar Genjang	a × t	2 × (a + b)
Belah Ketupat	1/2 × d1 × d2	4 × s
Layang-Layang	1/2 × d1 × d2	s + s + s + s
Lingkaran	π × r²	2 × π × r

Rumus Bangun Ruang Lengkap dan Contoh Soal

Bangun ruang adalah bangun yang memiliki volume atau isi yang dibatasi oleh sisi permukaannya. Nah, berikut merupakan kumpulan rumus bangun ruang yang digunakan untuk menghitung volume dan luas permukaannya lengkap beserta contoh soalnya.

A. Bangun Ruang Kubus

Kubus adalah bangun ruang yang dibatasi oleh enam sisi berbentuk persegi kongruen (sama dan sebangun) dan rusuk dengan ukuran sama panjang.

Rumus Bangun Ruang Kubus

Rumus Volume Kubus (V) = s × s × s

Rumus Luas Permukaan Kubus (L) = 6 × s × s

Contoh Soal
Sebuah kubus memiliki panjang rusuk 10 cm. Berapa volume dan luas permukaan kubus tersebut?

Pembahasan:
V = s x s x s
V = 10 x 10 x 10
V = 1.000 cm³

L = 6 x s x s
L = 6 x 10 x 10
L = 600 cm²

B. Bangun Ruang Balok

Balok adalah bangun ruang yang dibatasi oleh tiga pasang enam buah persegi dan persegi panjang, dimana setiap pasang persegi panjang saling sejajar dan berukuran sama.

Rumus Bangun Ruang Balok

Rumus Volume Balok (V) = p × l × t

Rumus Luas Permukaan Balok (L) = 2 ( p× l + l× t + p× t)

Contoh Soal
Sebuah balok memiliki ukuran panjang 10 cm, lebar 8 cm dan tinggi 5 cm. Berapa volume dan luas permukaan balok tersebut?

Pembahasan:
V = p x l x t
V = 10 x 8 x 5
V = 400 cm³

L = 2 (p x l + p x t + l x t)
L = 2 (10 x 8 + 10 x 5 + 8 x 5)
L = 2 (80 + 50 + 40)
L = 2 x 170
L = 340 cm²

C. Bangun Ruang Limas

Limas adalah bangun ruang yang dibatasi oleh sisi alas berbentuk segi-n dan sisi-sisi tegaknya berbentuk segitiga. Alas limas dapat berupa segitiga, segi empat, segi lima, segi enam dan setersunya.

Rumus Bangun Ruang Limas

Rumus Volume Limas (V) = 1/3 × luas alas × tinggi

Rumus Luas Permukaan Limas (L) = luas alas + luas seluruh sisi tegak

Contoh Soal
Sebuah limas segitiga memiliki luas alas 60 cm² dan luas sisi tegak 30 cm². Jika tinggi limas 10 cm, berapa volume dan luas permukaan limas tersebut?

Pembahasan:
V = 1/3 x luas alas x tinggi
V = 1/3 x 60 x 10
V = 1/3 x 600
V = 200 cm³

L = luas alas + luas seluruh sisi tegak
L = luas alas + (3 x luas sisi tegak)
L = 60 + (3 x 30)
L = 60 + 90
L = 150 cm²

D. Bangun Ruang Prisma

Prisma adalah bangun ruang yang dibatasi oleh sisi alas dan sisi atas berbentuk segi-n kongruen (sama dan sebangun) dan sisi tegak berbentuk persegi atau persegi panjang.

Rumus Bangun Ruang Prisma

Rumus Volume Prisma (V) = luas alas × tinggi

Rumus Luas Permukaan Prisma (L) = (2 × luas alas) + (keliling alas × tinggi)

Contoh Soal
Sebuah prisma persegi memiliki panjang sisi alas 10 cm dan tinggi prisma 15 cm. Berapa volume dan luas permukaan prisma tersebut?

Pembahasan:
V = luas alas x tinggi
V = (sisi x sisi) x tinggi
V = (10 x 10) x 15
V = 100 x 15
V = 1.500 cm³

L = (2 x luas alas) + (keliling alas x tinggi)
L = (2 x s x s) + (4 x s x tinggi)
L = (2 x 10 x 10) + (4 x 10 x 15)
L = 200 + 600
L = 800 cm²

E. Bangun Ruang Kerucut

Kerucut adalah bangun ruang yang dibatasi oleh sisi alas berbentuk lingkaran dan sisi selimut yang berbentuk irisan lingkaran (juring lingkaran). Selimut kerucut meruncing di bagian atasnya dan membentuk titik sudut (puncak kerucut).

Rumus Bangun Ruang Kerucut

Rumus Volume Kerucut (V) = 1/3 × π × r² × t

Rumus Luas Permukaan Kerucut (L) = π × r (r + s)

Contoh Soal
Sebuah kerucut memiliki jari-jari 7 cm dan tinggi 24 cm. Jika panjang garis pelukis kerucut adalah 25 cm, berapa volume dan luas permukaan kerucut tersebut?

Pembahasan:
V = 1/3 x π x r² x t
V = 1/3 x 22/7 x 7² x 24
V = 1/3 x 22/7 x 49 x 24
V = 1/3 x 3.696
V = 1.232 cm³

L = π x r (r + s)
L = 22/7 x 7 (7 + 25)
L = 22 x 32
L = 704 cm²

F. Bangun Ruang Tabung

Tabung adalah bangun ruang yang dibatasi oleh sisi alas dan sisi atas (tutup) berbentuk lingkaran kongruen (sama dan sebangun) dan sisi tegak berbentuk lengkungan persegi panjang.

Rumus Bangun Ruang Tabung

Rumus Volume Tabung (V) = π × r² × t

Rumus Luas Permukaan Tabung (L) = (2 × luas alas) + (keliling alas × tinggi)

Contoh Soal
Sebuah tabung memiliki jari-jari 7 cm dan tinggi 10 cm. Berapa volume dan luas permukaan tabung tersebut?

Pembahasan:
V = π x r² x t
V = 22/7 x 7² x 10
V = 22/7 x 49 x 10
V = 154 x 10
V = 1.540 cm³

L = 2 x π x r x (r + t)
L = 2 x 22/7 x 7 x (7 + 10)
L = 44 x 17
L = 748 cm²

G. Bangun Ruang Bola

Bola adalah bangun ruang yang dibatasi oleh sebuah sisi lengkung. Bangun bola memiliki bentuk bulat sempurna yang tersusun oleh tak terhingga lingkaran yang mempunyai jari-jari dan pusat lingkaran yang sama.