Cara Menentukan Gabungan Himpunan – Dalam pelajaran matematika, terdapat materi tentang himpunan. Materi himpunan ini melibatkan perhitungan gabungan, irisan, selisih, dan komplemen. Nah, pada kesempatan kali ini akan dibahas bagaimana cara menentukan gabungan pada suatu himpunan.
Untuk menentukan gabungan dari dua himpunan atau lebih, kita perlu mengetahui apa itu gabungan himpunan. Gabungan dari dua himpunan A dan B merupakan suatu himpunan yang anggotanya terdiri dari anggota himpunan A atau anggota himpunan B atau anggota kedua-duanya. Gabungan himpunan dituliskan dengan simbol ∪ (Union).
Sebagai contoh, A ∪ B memiliki arti himpunan yang anggotanya merupakan anggota himpunan A atau anggota himpunan B. Rumus gabungan himpunan A dan B dinotasikan dengan:
A ∪ B = {x│x ∈ A atau x ∈ B}
Keterangan :
∪ : Simbol untuk menyatakan gabungan.
∈ : Simbol untuk menyatakan keanggotaan.
│ : simbol yang artinya dimana
A ∪ B : dibaca “A gabungan B”
{ x│x ∈ A atau x ∈ B} : dibaca “x dimana x anggota A atau x anggota B”
Contoh:
A = {1, 2, 3, 4}
B = {4, 5, 6, 7}
Jika himpunan A digabungkan dengan himpunan B, maka akan diperoleh sebuah himpunan baru yang anggotanya 1, 2, 3, 4, 5, 6, 7. Sehingga, jika dituliskan sebagai himpunan gabungan menjadi : A ∪ B = {1, 2, 3, 4, 5, 6, 7}. A ∪ B dibaca himpunan A gabungan himpunan B. Dalam diagram venn, A ∪ B ditunjukkan oleh gambar berikut ini.

Cara Menentukan Gabungan Himpunan
Untuk menentukan gabungan pada dua himpunan atau lebih, kita dapat menggunakan langkah-langkah sebagai berikut:
- Langkah 1: Tentukan semua hal yang diketahui dan yang dipertanyakan pada soal.
- Langkah 2: Tuliskan semua anggota dari masing-masing himpunan, jika terdapat anggota yang sama, cukup menuliskan salah satunya saja.
- Langkah 3: Menentukan himpunan gabungan.
Agar lebih jelas memahami langkah-langkah di atas, silahkan perhatikan beberapa contoh soal berikut ini.
Contoh Soal :
- Tentukan himpunan gabungan dari himpunan :
A = {1, 2, 3, 4, 5, 6}
B = {4, 5, 6, 7, 8, 9}
Jawaban:
Langkah 1: Menentukan semua hal yang diketahui dan yang dipertanyakan pada soal.
A = {1, 2, 3, 4, 5, 6}
B = {4, 5, 6, 7, 8, 9}
Ditanyakan :
A ∪ B = { ..? }
Langkah 2: Tuliskan semua anggota dari masing-masing himpunan, jika terdapat anggota yang sama, cukup tuliskan salah satunya saja.
A = {1, 2, 3, 4, 5, 6}
B = {4, 5, 6, 7, 8, 9}
Anggota yang sama dari himpunan A dan B adalah 4, 5 ,6. Sehingga diperoleh hasil: 1, 2, 3, 4, 5, 6, 7, 8, 9.
Langkah 3: Menentukan himpunan gabungan.
Melihat dari langkah kedua, maka himpunan gabungan dari A = {1, 2, 3, 4, 5, 6} dan B = {4, 5, 6, 7, 8, 9} adalah : A ∪ B = {1, 2, 3, 4, 5, 6, 7, 8, 9}.
- Perhatikan gambar di bawah ini!
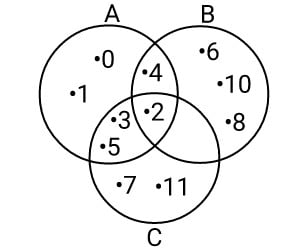
Tentukan!
a. A ∪ B
b. A ∪ C
c. B ∪ C
d. A ∪ B ∪ C
Jawaban:
Langkah 1 : Tentukan semua hal yang diketahui dan yang dipertanyakan pada soal.
A = {0, 1, 2, 3, 4, 5}
B = {2, 4, 6, 8, 10}
C = {2, 3, 5, 7, 11}
Ditanyakan :
a. A ∪ B = { ..? }
b. A ∪ C = { ..? }
c. B ∪ C = { ..? }
d. A ∪ B ∪ C = { ..? }
Langkah 2: Tuliskan semua anggota dari masing-masing himpunan, jika terdapat anggota yang sama, kita cukup menuliskan salah satunya saja.
A ∪ B = {0, 1, 2, 3, 4, 5, 6, 8, 10}
A ∪ C = {0, 1, 2, 3, 4, 5, 7, 11}
B ∪ C = {2, 3, 4, 5, 6, 7, 8, 10, 11}
Anggota yang sama dari himpunan A, B, dan C adalah 2, 3, 4, dan 5. Maka A ∪ B ∪ C = {0, 1, 2, 3, 4, 5, 6, 7, 8, 10, 11}
Langkah 3: Menentukan himpunan gabungan.
Melihat dari langkah kedua, untuk menjawab pertanyaan contoh soal pada gambar di atas dari A = {0, 1, 2, 3, 4, 5}, B = {2, 4, 6, 8, 10}, dan C = {1, 3, 5, 7, 9} adalah :
a. A ∪ B = {0, 1, 2, 3, 4, 5, 6, 8, 10}
b. A ∪ C = {0, 1, 2, 3, 4, 5, 7, 11}
c. B ∪ C = {2, 3, 4, 5, 6, 7, 8, 10, 11}
d. A ∪ B ∪ C = {0, 1, 2, 3, 4, 5, 6, 7, 8, 10, 11}
Kesimpulan
Untuk menentukan gabungan dari dua himpunan atau lebih, dapat dilakukan dengan cara menuliskan seluruh anggota dari masing-masing himpunan. Jika terdapat anggota yang sama, maka kita cukup menuliskan satu saja.
Demikianlah pembahasan mengenai cara menentukan gabungan himpunan dalam pelajaran matematika. Semoga bermanfaat.
Baca Lagi :