Pecahan: Pengertian, Jenis, Rumus, dan Contoh Soal – Salah satu bilangan yang dipelajari pada matematika bilangan pecahan. Apakah itu bilangan pecahan? Seperti apa contoh bilangan pecahan? bagaimana cara menghitung pecahan? Untuk mengetahui jawabannya, silahkan simak pembahasan berikut ini tentang pengertian, jenis, rumus, dan contoh soal mengenai pecahan.
Pengertian Pecahan
Pecahan adalah suatu bilangan yang terdiri dari dua angka, yang ditulis dalam bentuk a/b, di mana a dan b merupakan bilangan bulat, serta nilai b tidak sama dengan nol (0). a disebut pembilang pecahan dan b disebut penyebut pecahan. Apa itu pembilang? Apa itu penyebut?
Pembilang adalah bilangan pecahan yang letaknya di atas atau bilangan yang dibagi, sedangkan penyebut merupakan bilangan pembagi yang letaknya di bawah.
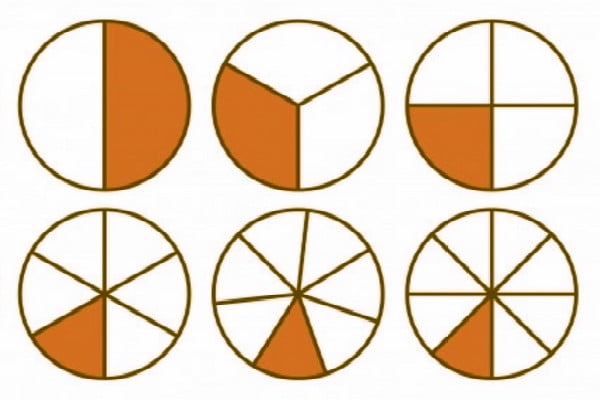
Nilai pembilang dan penyebut pada bilangan pecahan adalah saling prima, artinya tidak ada faktor/pembagi yang bisa membagi pembilang dan penyebut sekaligus. Perhatikan gambar berikut ini.
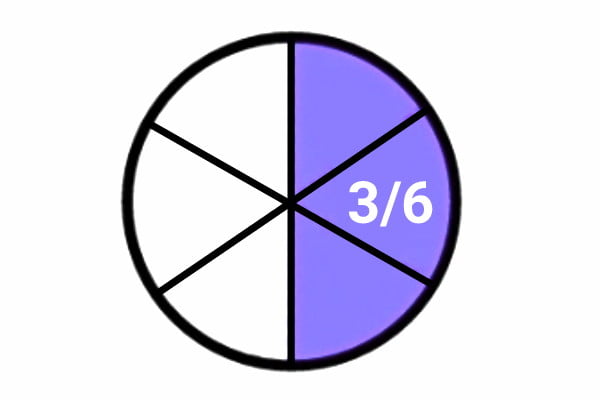
Bagian yang diarsir memiliki besar 3/6 bagian dari keseluruhan bagian (lingkaran). Oleh sebab itu, pecahan juga dapat diartikan sebagai perbandingan suatu bagian dengan keseluruhannya.
Jenis-Jenis Pecahan
Berikut merupakan jenis-jenis bentuk pecahan dan contohnya masing-masing.
1. Pecahan Biasa
Pecahan biasa adalah bentuk pecahan yang hanya terdiri dari pembilang dan penyebut saja. Pecahan biasa ditulis dalam bentuk a/b, dimana a adalah pembilang dan b adalah penyebut.
Contoh pecahan biasa:
1/3 = pecahan biasa, dimana 1 sebagai pembilang dan 3 sebagai penyebut
2/5 = pecahan biasa, dimana 2 sebagai pembilang dan 5 sebagai penyebut
2. Pecahan Murni Dan Tak Murni
Berdasarkan nilai pembilang dan penyebutnya, pecahan dibedakan menjadi dua jenis, yaitu pecahan murni dan tidak murni. Disebut pecahan murni jika suatu pecahan nilai pembilangnya lebih kecil dari pada penyebutnya, sedangkanpecahan tak murni adalah pecahan yang nilai pembilangnya lebih besar dari pada penyebut.
Contoh pecahan murni:
1/2 = pecahan murni, nilai pembilang (1) lebih kecil dari penyebut (2)
2/3 = pecahan murni, nilai pembilang (2) lebih kecil dari penyebut (3)
Contoh pecahan tidak murni:
5/4 = pecahan tak murni, nilai pembilang (5) lebih besar dari penyebut (4)
4/3 = pecahan tak murni, nilai pembilang (4) lebih besar dari penyebut (3)
3. Pecahan Campuran
Pecahan campuran adalah bilangan pecahan yang terdiri dari bilangan bulat dan pecahan biasa. Pecahan campuran dituliskan dalam bentuk a b/c, dimana a merupakan bilangan bulat dan b/c merupakan pecahan biasa.
Contoh pecahan campuran:
1 1/4 = pecahan campuran, dimana 1 adalah bilangan bulat dan 1/4 merupakan pecahan biasa
2 1/2 = pecahan campuran, dimana 2 adalah bilangan bulat dan 1/4 merupakan pecahan biasa
Cara Mengubah Pecahan Campuran ke Pecahan Biasa
Pecahan campuran dapat diubah menjadi pecahan biasa, caranya yaitu dengan mengalikan bagian bulat dengan penyebut pecahan, kemudian hasilnya dijumlahkan dengan pembilangnya. Hasil tersebut dijadikan pembilang pecahan, sedangkan untuk penyebutnya tetap dari pecahan awalnya.
Contoh:
1 2/3 diubah ke pecahan biasa
Pembahasan:
mengalikan bagian bulat dengan penyebut pecahan = 1 x 3 = 3
kemudian hasilnya (3) dijumlahkan dengan pembilangnya = 3 + 2 = 5
hasil tersebut dijadikan pembilang (5), penyebutnya tetap dari pecahan awalnya = 5/3
4. Pecahan Desimal
Pecahan desimal merupakan bentuk pecahan yang memiliki penyebut 10, 100, 1000, dan seterusnya. Bentuk pecahan desimal dituliskan dengan menggunakan tanda koma (,).
Contoh pecahan desimal:
0,5 = bilangan desimal dari 5/10
0,05 = bilangan desimal dari 5/100
0,005 = bilangan desimal dari 5/1000
Cara Mengubah Pecahan Desimal ke Pecahan Biasa
Pecahan desimal dapat diubah ke pecahan biasa, caranya yaitu dengan mengubah penyebut pecahan menjadi 10, 100, 1000, dan seterusnya sesuai banyaknya angka yang ada di belakang koma pada pecahan desimal.
Contoh:
0,5 diubah ke pecahan biasa
0,5 = 5/10 = 1/2
5. Pecahan Bentuk Persen
Persen adalah bentuk bilangan pecahan khusus uang memiliki penyebut 100. Penulisan pecahan persen ditulis menggunakan tanda persen (%).
Contoh pecahan persen:
10% (dibaca 10 persen) = bentuk persen dari 10/100
25% (dibaca 25 persen) = bentuk persen dari 25/100
Cara Mengubah Persen ke Pecahan Biasa dan Desimal
Pecahan persen dapat diubah ke pecahan biasa dan pecahan desimal, caranya yaitu dengan mengubah penyebut pecahan menjadi 100.
Contoh:
50% diubah ke pecahan biasa
50% = 50/100 = 1/2
50% diubah ke pecahan desimal
50% = 50/100 = 5/10 = 0,5
6. Pecahan Senilai
Pecahan senilai adalah pecahan yang nilainya tidak akan berubah meskipun pembilang dan penyebutnya dikalikan atau dibagi dengan bilangan yang sama. Dengan kata lain, dua buah pecahan yang berbeda dapat dikatakan senilai jika nilai perbandingannya tetap.
Pecahan senilai dapat diperoleh dengan cara membagi atau mengkalikan pembilang dan penyebut pecahan dengan bilangan yang sama.
Contoh pecahan senilai:
1/2 ; 2/4 ; 3/6 ; 4/8
Pembahasan:
1/2 x 2/2 = 2/4
1/2 x 3/3 = 3/6
1/2 x 4/4 = 4/8
2/4 : 2/2 = 1/2
3/6 : 3/3 = 1/2
4/8 : 4/4 = 1/2
Rumus-Rumus Pecahan
1. Penjumlahan Pecahan
a. Penjumlahan Pecahan Berpenyebut Sama
Untuk menghitung penjumlahan pecahan yang memiliki penyebut sama, maka dapat dilakukan dengan cara menjumlahkan bagian pembilangnya saja, sedangkan penyebutnya tetap.
Contoh:
1/4 + 2/4 = 3/4
b. Penjumlahan Pecahan Beda Penyebut
Jika dua buah pecahan atau lebih memiliki penyebut berbeda, maka untuk menjumlahkannya harus menyamakan penyebutnya terlebih dahulu.
Contoh:
1/2 + 1/3 = …
1/2 = 3/6
1/3 = 2/6
1/2 + 1/3 = 3/6 + 2/6 = 5/6
2. Pengurangan Pecahan
a. Pengurangan Pecahan Berpenyebut Sama
Untuk menghitung pengurangan pecahan yang memiliki penyebut sama, maka dapat dilakukan dengan cara mengurangi bagian pembilangnya saja, sedangkan penyebutnya tetap.
Contoh:
3/4 – 2/4 = 1/4
b. Pengurangan Pecahan Beda Penyebut
Jika dua buah pecahan atau lebih memiliki penyebut berbeda, maka untuk melakukan pengurangan harus menyamakan penyebutnya terlebih dahulu.
Contoh:
1/2 – 1/3 = …
1/2 = 3/6
1/3 = 2/6
1/2 – 1/3 = 3/6 – 2/6 = 1/6
3. Perkalian Pecahan
Untuk menghitung perkalian pada pecahan, caranya sangat mudah. Rumusnya adalah kalikan pembilang dengan pembilang, lalu kalikan penyebut dengan penyebut.
Contoh:
1/2 x 1/4 = 1/8
2/3 x 1/3 = 2/9
3/4 x 4/5 = 12/20 = 3/5
4. Pembagian Pecahan
Untuk menghitung pembagian pecahan, caranya yaitu dengan membalikan posisi pembilang sebagai penyebut dan penyebut sebagai pembilang pada pecahan pembagi, lalu mengubah operasi pembagian menjadi perkalian.
Contoh:
1/2 : 1/3 = 1/2 x 3/1 = 3/2
5. Membandingkan Pecahan
Membandingkan pecahan adalah menentukan hubungan antara dua buah pecahan dengan menggunakan lambang lebih dari (>), kurang dari (<), atau sama dengan (=).
a. Membandingkan Dua Pecahan Sejenis
Untuk membandingkan dua pecahan sejenis (memiliki penyebut sama), cukup dengan membandingkan bagian pembilangnya saja dan menyimpulkan apakah lebih besar, lebih keci atau sama dengan.
Contoh:
1/4 … 3/4
Bandingkan pembilang antara 1 dan 4 (1 lebih kecil dari 4)
Maka, 1/4 < 3/4
b. Membandingkan Dua Pecahan Tidak Sejenis
Untuk membandingkan pecahan tidak sejenis, caranya yaitu dengan menyamakan penyebutnya terlebih dahulu agar menjadi pecahan sejenis. Atau dapat juga dengan cara mengalikan pembilang pecahan pertama dengan penyebut pecahan kedua dan sebaliknya.
Contoh:
1/2 … 1/3
Cara 1: Mengubah menjadi pecahan sejenis
1/2 = 3/6
1/3 = 2/6
3/6 > 2/6
1/2 > 1/3
Cara 2: Mengalikan pembilang pecahan pertama dengan penyebut pecahan kedua dan sebaliknya
1/2 … 1/3
(1 x 3) … (1 x 2)
3 … 2
3 > 2
1/2 > 1/3
6. Menyederhanakan Pecahan
Untuk menyederhanakan suatu pecahan dapat dilakukan melalui dua cara/metode. Berikut penjelasannya.
a. Menyederhanakan Pecahan Metode FPB
Cara pertama adalah membagi dengan nilai FPB (Faktor Persekutuan Terbesar) dari angka pembilang dan penyebut.
Contoh:
Menyederhanakan pecahan 18/24
Langkah:
Mencari FPB dari 18 dan 24
Faktor 18 = 1, 2, 3, 6, 9, 18
Faktor 24 = 1, 2, 3, 4, 6, 8, 12, 24
FPB dari 18 dan 24 = 6
18/24 = (18 : 6) / (24 : 6) = 3/4
b. Menyederhanakan Pecahan Metode Pembagian
Cara kedua adalah membagi secara terus menerus antara pembilang dan penyebut dengan bilangan yang sama sampai tidak dapat dibagi lagi.
Contoh:
Menyederhanakan pecahan 18/24
18/24 = (18 : 2) / (24 : 2) = 9/12
9/12 = (9 : 3) / (12 : 3) = 3/4
7. Mengurutkan Pecahan
Mengurutkan pecahan adalah menyusun urutan dari beberapa pecahan dari urutan terkeci sampai terbesar atau sebaliknya.
a. Mengurutkan Pecahan Berpenyebut Sama
Mengurutkan pecahan berpenyebut sama adalah menyusun beberapa pecahan yang memiliki penyebut sama dari urutan terkecil ke terbesar atau sebaliknya. Caranya yaitu dengan menentukan bagian pembilangnya saja.
Contoh:
Urutkan pecahan 1/5 ; 3/5 ; 2/5
Perhatikan nilai pembilangnya (1, 3, 2)
Urutan pecahan dari terkecil ke terbesar = 1/5 ; 2/5 ; 3/5
Urutan pecahan dari terbesar ke terkecil = 3/5 ; 2/5 ; 1/5
b. Mengurutkan Penyebut Beda Penyebut
Mengurutkan pecahan beda penyebut adalah menyusun beberapa pecahan yang memiliki penyebut berbeda dari urutan terkecil ke terbesar atau sebaliknya. Caranya yaitu dengan menyamakan penyebutnya.
Contoh:
Urutkan pecahan 1/2 ; 1/3 ; 1/4
Menyamakan penyebutnya menjadi 12
1/2 = 6/12
1/3 = 4/12
1/4 = 3/12
Urutan pecahan dari terkecil ke terbesar = 1/4 ; 1/3 ; 1/2
Urutan pecahan dari terbesar ke terkecil = 1/2 ; 1/3 ; 1/4
c. Mengurutkan Pecahan Berbeda Jenis
Mengurutkan pecahan berbeda jenis adalah menyusun beberapa jenis pecahan berbeda, seperti desimal, persen dan pecahan biasa urutan terkecil ke terbesar atau sebaliknya. Caranya yaitu dengan mengubahnya menjadi bentuk pecahan yang sama.
Contoh:
Urutkan pecahan 3/4 ; 0,25 ; 50%
Mengubahnya menjadi bentuk yang sama, misalkan diubah ke pecahan biasa
3/4 = 3/4
0,25 = 25/100 = 1/4
50% = 50/100 = 1/2
Menyamakan penyebutnya menjadi 4
3/4 = 3/4
1/4 = 1/4
1/2 = 2/4
Urutan pecahan dari terkecil ke terbesar = 0,25 ; 50% ; 3/4
Urutan pecahan dari terbesar ke terkecil = 3/4 ; 50% ; 0,25
Contoh Soal Pecahan
1. Sebutkan jenis-jenis pecahan dan berikan contohnya masing-masing!
Pembahasan:
Pecahan biasa, contohnya = 1/2 ; 1/3 ; 1/4
Pecahan campuran, contohnya = 1 1/2 ; 2 1/4 ; 5 3/4
Pecahan desimal, contohnya = 0,1 ; 0,25 ; 0,8
Pecahan persen, contohnya = 10% ; 25% ; 50%
Pecahan senilai, contohnya = 1/2 = 2/4 = 3/6
2. Hitunglah operasi pecahan berikut ini dan sederhanakan hasilnya!
a. 3/4 + 2/4
b. 7/8 – 6/8
Pembahasan:
a. 3/4 + 2/4 = 5/4 = 1 1/4
b. 7/8 – 3/8 = 4/8 = 1/2
3. Hitunglah operasi perkalian dan pembagian pecahan berikut ini!
a. 3/5 x 1/2
b. 1/2 : 1/4
Pembahasan:
a. 3/5 x 1/2 = 3/10
b. 1/2 : 1/4 = 1/2 x 4/1 = 4/2 = 2
4. Berikan tanda yang tepat (<, >, atau =) untuk membandingkan pecahan dibawah ini!
a. 1/4 … 3/4
b. 1/2 … 2/8
c. 1/3 … 9/27
Pembahasan:
a. 1/4 < 3/4 b. 1/2 > 2/8 (4/8 > 2/8)
c. 1/3 = 9/27 (9/27 = 9/27)
5. Urutkan pecahan dari yang terkecil ke terbesar antara 1,25 ; 75% ; 1/4 ; 4/8
Pembahasan:
Diubah menjadi pecahan biasa berpenyebut 4
1,25 = 125/100 = 5/4
75% = 75/100 = 3/4
1/4 = 1/4
4/8 = 2/4
Urutkan dari yang terkecil ke terbesar adalah = 1/4 ; 4/8 ; 75% ; 1,25
Demikian pembahasan mengenai pengertian, jenis, rumus dan contoh soal tentang pecahan. Semoga bermanfaat.
Baca Lagi :