Kubus: Pengertian, Unsur, Sifat, Jaring Dan Rumus Kubus – Salah satu jenis bangun ruang adalah kubus. Kubus memiliki karaktersistik yang berbeda dengan bangun ruang lainnya. Pada kesempatan kali ini akan dibahas secara lengkap mengenai pengertian kubus, unsur-unsur kubus, sifat kubus, jaring-jaring kubus, dan rumus kubus.
Pengertian Kubus
Apa itu kubus? Kubus adalah bangun ruang tiga dimensi yang dibatasi oleh enam sisi berbentuk persegi. Bentuk persegi pada sisi kubus memiliki ukuran sama besar (kongruen). Kubus disebut juga sebagai bentuk geometri enam beraturan.
Kubus memiliki 6 sisi, 12 rusuk dan 8 titik sudut. Sisi kubus berbentuk persegi dan rusuk-rusuk kubus memiliki ukuran sama panjang. Sedangkan titik sudut kubus terbentuk oleh pertemuan antara tiga rusuk kubus.
Dalam kehidupan sehari-hari, banyak ditemui benda yang memiliki bentuk kubus. Salah satunya yaitu dadu, Dadu adalah kotak yang memiliki titik-titik angka pada sisinya yang biasanya digunakan pada permainan ular tangga.
Unsur-Unsur Kubus
Setiap bangun ruang memiliki unsur-unsur pembentuk ruangannya. Berikut akan dijelaskan apa saja unsur-unsur kubus. Perhatikan gambar berikut ini.

1. Sisi Kubus
Sisi kubus adalah daerah yang membatasi bagian dalam kubus dengan ruangan di sekitarnya. Kubus mempunyai 6 buah sisi yang keseluruhannya berbentuk persegi. Sisi-sisi kubus ditunjukan oleh:
- Sisi depan (ABFE)
- Sisi belakang (DCGH)
- Sisi atas (EFGH)
- Sisi bawah (ABCD)
- Sisi samping kiri (BCGF)
- Sisi samping kanan (ADHE)
2. Rusuk Kubus
Rusuk kubus adalah garis-garis pembentuk kubus. Rusuk kubus merupakan pembatas tiap-tiap sisi kubus. Kubus mempunyai 12 rusuk yang sama panjang. Rusuk-rusuk kubus ditunjukan oleh:
- Rusuk alas = AB, BC, CD, DA
- Rusuk tinggi = AE, BF, CG, DH
- Rusuk atas = EF, FG, GH, HE
3. Titik Sudut Kubus
Titik sudut kubus adalah titik pertemuan antara tiga rusuk kubus. Kubus mempunyai 8 titik sudut. Setiap rusuk kubus yang bertemu pada titik sudut berbentuk sudut siku-siku. Titik rusuk kubus ditunjukan oleh huruf A, B, C, D, E, F, G, H.
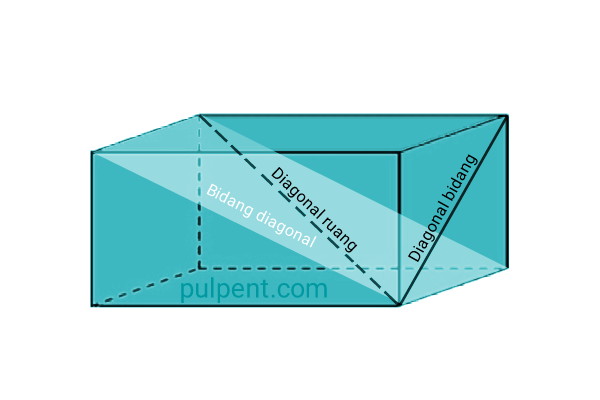
4. Diagonal Bidang Kubus
Diagonal bidang kubus adalah garis diagonal yang terbentuk pada sisi kubus. Tiap-tiap sisi kubus memiliki 2 garis diagonal. Sehingga, kubus mempunyai 12 diagonal bidang. Diagonal bidang kubus ditunjukan oleh: AF, BE, BG, FC, CH, DG, AH, DE, BD, AC, EG, HG.
5. Diagonal Ruang Kubus
Diagonal ruang kubus adalah ruas garis yang menghubungkan dua titik sudut kubus yang saling berhadapan. Kubus mempunyai 4 diagonal ruang yang sama panjang. Keempat diagonal ruang kubus bertemu pada satu titik tepat di tengah-tengah ruangan kubus (titik pusat kubus). Diagonal ruang kubus ditunjukan oleh:
- Diagonal BH
- Diagonal DF
- Diagonal AG
- Diagonal EC
6. Bidang Diagonal Kubus
Bidang diagonal kubus adalah bidang yang terbentuk oleh dua garis diagonal bidang dan dua garis rusuk kubus. Kubus mempunyai 6 bidang diagonal. Bidang diagonal kubus memiliki luas yang sama. Bidang diagonal kubus ditunjukan oleh:
- Bidang diagonal ACGE
- Bidang diagonal BCHE
- Bidang diagonal CDEF
- Bidang diagonal ADGF
- Bidang diagonal ABGH
- Bidang diagonal BDHF
Sifat-Sifat Kubus
Kubus memiliki ciri-ciri yang berbeda dengan bangun ruang lainnya. Ciri-ciri kubus menyatakan sifat-sifat kubus. Berikut merupakan sifat-sifat kubus:
- Memiliki 6 buah sisi yang luasnya sama
- Keenam sisi kubus berbentuk persegi
- Memiliki 8 buah titik sudut
- Memiliki 12 buah rusuk sama panjang
- Memiliki 12 diagonal bidang sama panjang
- Memiliki 4 diagonal ruang sama panjang
- Memiliki 6 bidang diagonal yang luasnya sama
Jaring-Jaring Kubus
Jaring-jaring adalah gabungan dari beberapa bangun datar pembentuk bangun ruang. Setiap bangun ruang memiliki jaring-jaring yang berbeda. Begitu juga dengan jaring-jaring kubus.
Jaring-jaring kubus terdiri dari enam buah bangun datar persegi yang sama besar. Kubus memiliki pola jaring-jaring sebanyak 11 buah. Berikut merupakan contoh gambar jaring-jaring kubus.

Pada gambar jaring-jaring kubus di atas, terdapat bentuk persegi dengan warna biru dan kuning. Persegi dengan warna biru adalah sisi alas kubus dan persegi dengan warna kuning adalah sisi atas kubus.
Rumus Kubus
A. Rumus Volume Kubus
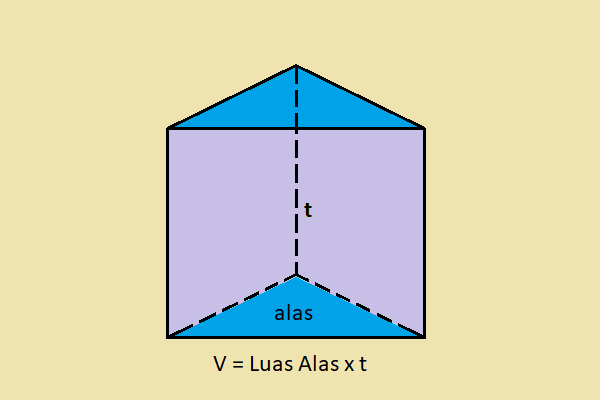
Volume kubus adalah seberapa besar ruangan di dalam kubus yang mampu ditempati. Volume kubus dapat dihitung dengan mengkalikan luas alas dengan tingginya.
Alas kubus adalah persegi yang panjang sisinya merupakan rusuk kubus. Sedangkan tinggi kubus juga merupakan panjang rusuk kubus. Dengan begitu, rumus untuk menghitung volume kubus adalah:
| V = s x s x s |
Keterangan:
V = volume kubus
s = rusuk kubus
Satuan volume adalah satuan panjang kubik, contohnya: m³, cm³, mm³.
Contoh Soal
Diketahui suatu kubus memiliki panjang rusuk 10 cm. Berapa volume kubus tersebut?
Penyelesaian:
V = s x s x s
V = 10 x 10 x 10
V = 1000 m³.
B. Rumus Luas Permukaan Kubus
Perhatikan gambar jaring-jaring kubus di atas, kubus terdiri dari enam buah persegi yang sama besar. Nah, jumlah dari luas keenam persegi itulah yang dinamakan luas permukaan kubus. Jadi, luas permukaan kubus adalah luas seluruh sisi kubus.
Untuk menghitung luas permukaan kubus, maka kita juga harus mengetahui rumus luas persegi. Rumus luas persegi adalah sisi x sisi. Kubus memiliki 6 buah sisi berbentuk persegi. Dengan begitu, rumus untuk menghitung luas permukaan kubus adalah:
| L = 6 x s x s |
Keterangan:
L = luas permukaan kubus
s = rusuk kubus
Satuan luas permukaan adalah satuan panjang persegi, contoh: m², cm², mm².
Contoh Soal
Diketahui suatu kubus mempunyai panjang rusuk 10 cm. Berapa luas permukaan kubus tersebut?
Penyelesaian:
L = 6 x s x s
L = 6 x 10 x 10
L = 600 m².
C. Rumus Keliling Kubus
Keliling kubus adalah panjang seluruh rusuk kubus. Kubus memiliki jumlah rusuk sebanyak 12 buah dengan ukuran sama panjang. Dengan begitu, rumus untuk menghitung keliling kubus adalah:
| K = 12 x s |
Keterangan:
K = keliling kubus
s = rusuk kubus
Contoh Soal
Diketahui suatu kubus mempunyai panjang rusuk 10 cm. Berapa keliling kubus tersebut?
Penyelesaian:
K = 12 x s
K = 12 x 10
K = 120 cm.
D. Rumus Rusuk Kubus
Panjang rusuk kubus dapat digunakan untuk menghitung volume, luas permukaan, dan keliling kubus. Lalu bagaimana jika akan mencari panjang rusuk kubus yang telah diketahui hal-hal tersebut? Berikut Penjelasannya.
Rusuk Kubus Jika Diketahui Volumenya
Rumus untuk menghitung volume kubus adalah s x s x s atau s³. Dari rumus tersebut, maka untuk mencari panjang rusuk sebuah kubus yang telah diketahui volumenya adalah:
| s = ³√V |
Contoh Soal
Diketahui volume sebuah kubus adalah 3.375 cm³. Berapa panjang rusuk kubus tersebut?
Penyelesaian:
s = ³√V
s = ³√3.375
s = 15 cm.
Rusuk Kubus Jika Diketahui Luas Permukaannya
Rumus untuk menghitung luas permukaan kubus adalah 6 x s x s atau 6 x s². Dari rumus tersebut, maka untuk mencari panjang rusuk kubus yang telah diketahui luas permukaannya adalah:
| s = √(L : 6) |
Contoh Soal
Diketahui luas permukaan sebuah kubus adalah 2.400 cm². Berapa panjang rusuk kubus tersebut?
Penyelesaian:
s = √(L : 6)
s = √(2.400 : 6)
s = √400
s = 20 cm.
Rusuk Kubus Jika Diketahui Kelilingnya
Rumus untuk menghitung keliling kubus adalah 12 x s. Dari rumus tersebut, maka untuk mencari panjang rusuk kubus yang telah diketahui kelilingnya adalah:
| s = K : 12 |
Contoh Soal
Diketahui keliling sebuah kubus adalah 300 cm. Berapa panjang rusuk kubus tersebut?
Penyelesaian:
s = K : 12
s = 300 : 12
s = 25 cm.
Demikianlah pembahasan mengenai lengkap mengenai pengertian, unsur, sifat, jaring-jaring dan rumus kubus. Silahkan share jika bermanfaat.
Baca Lagi :