Balok: Ciri, Rumus Volume, Luas Permukaan dan Keliling Balok – Artikel sebelumnya telah dibahas mengenai bangun kubus. Pada kesempatan kali ini akan dipelajari mengenai bangun ruang lainnya, yaitu balok.
Balok memiliki sisi permukaan berbentuk segi empat, tetapi ukurannya tidak sama. Berbeda dengan kubus yang seluruh sisinya berukuran sama.
Agar lebih jelas tentang bangun balok, silahkan simak pembahasan berikut ini mengenai pengertian, bagian-bagian, ciri-ciri, jaring-jaring, rumus volume, rumus luas permukaan, rumus keliling dan rumus rusuk balok beserta contoh soal dan cara penyelesaiannya.
Pengertian Balok
Balok adalah bangun ruang tiga dimensi yang memiliki volume atau isi. Bangun ruang balok dibatasi oleh tiga pasang sisi berbentuk persegi atau persegi panjang dengan setidaknya terdapat satu pasang sisi yang memiliki ukuran berbeda.
Balok merupakan bentuk tiga dimensi. Dalam kehidupan sehari-hari, terdapat banyak benda yang berbentuk balok, seperti lemari baju, kulkas, televisi, smartphone dan lain sebagainya.
Dalam bahasa inggris, balok disebut cuboids. Bangun ruang balok mempunyai 6 buah sisi, 12 buah rusuk dan 8 buah titik sudut. Berikut merupan contoh gambar bangun balok.
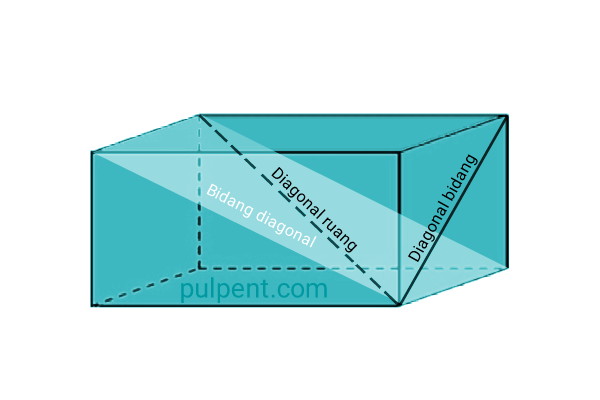
Bagian-Bagian Balok
Dari gambar balok di atas, kita dapat menentukan bagian-bagian balok. Berikut merupakan bagian-bagian penyusun balok.
- Sisi Balok, adalah bidang yang membatasi ruangan balok
- Rusuk Balok, adalah garis perpotongan antar sisi-sisi balok
- Titik Sudut Balok, adalah titik pertemuan antara tiga buah rusuk balok atau lebih
- Diagonal Bidang Balok, adalah diagonal yang terbentuk pada sisi-sisi balok
- Diagonal Ruang Balok, adalah diagonal yang terbentuk oleh dua titik sudut balok yang saling berhadapan
- Bidang Diagonal Balok, adalah sebuah bidang yang terbentuk oleh dua diagonal bidang yang sejajar dan dua rusuk balok yang sejajar
Ciri-Ciri Balok
Balok berbeda dengan kubus. Berikut merupakan ciri-ciri dan sifat-sifat balok.
- Balok mempunyai 6 sisi berbentuk persegi dan persegi panjang
- Sisi balok terdiri dari 3 pasang sisi sejajar dan kongruen
- Sisi balok berbentuk persegi dan persegi panjang
- Balok mempunyai 12 rusuk
- Rusuk balok terdiri dari 4 rusuk panjang, 4 rusuk lebar, dan 4 rusuk tinggi
- Rusuk-rusuk yang sejajar memiliki ukuran sama panjang
- Balok mempunyai 8 titik sudut
- Balok mempunyai 12 diagonal bidang, terdiri dari 6 pasang diagonal sama panjang
- Balok mempunyai 4 diagonal ruang yang sama panjang
- Balok mempunyai 6 buah bidang diagonal
- Bidang diagonal balok berbentuk persegi panjang
Jaring-Jaring Balok
Jaring-jaring adalah pola berbentuk gabungan dari beberapa bentuk bangun penyusun bangun ruang. Jaring-jaring balok terdiri dari gabungan enam buah persegi dan persegi panjang.
Untuk menemukan rangkaian jaring-jaring balok, dapat dilakukan dengan cara membuka balok dan merentangkannya pada rusuk-rusuknya.
Balok memiliki pola jaring-jaring sebanyak 54 buah. Perlu diketahui bahwa tidak semua gabungan dari persegi dan persegi panjang dapat membentuk balok. Berikut merupakan contoh gambar jaring-jaring balok.

Gambar pola jaring-jaring balok di atas memiliki tiga pasang warna yang berbeda. Warna-warna yang sama adalah sisi balok yang berhadapan dan sejajar.
Rumus Volume Balok

Volume balok adalah seberapa besar ruangan di dalam balok yang dapat ditempati. Volume balok diukur dalam unit kubik. Untuk menghitung volume balok, kita harus mengetahui dimensi panjang, lebar dan tinggi balok. Secara matematis, rumus volume balok adalah:
| Rumus Volume Balok (V) = p x l x t |
Keterangan:
V = volume balok
p = panjang balok
l = lebar balok
t = tinggi balok
Contoh Soal: Cara Menghitung Volume Balok
Sebuah balok memiliki ukuran panjang 10 cm, lebar 8 cm dan tinggi 5 cm. Berapa volume balok tersebut?
Penyelesaian:
V = p x l x t
V = 10 x 8 x 5
V = 400 cm³
Jadi, volume balok tersebut adalah 400 cm³.
Rumus Luas Permukaan Balok
Luas permukaan balok adalah jumlah luas seluruh bidang permukaan balok. Luas balok diukur dalam unit luas persegi. Secara matematis, rumus luas permukaan balok adalah:
| Rumus Luas Permukaan Balok (L) = 2 x (p x l + p x t + l x t) |
Keterangan:
L = luas permukaan balok
p = panjang balok
l = lebar balok
t = tinggi balok
Contoh Soal: Cara Menghitung Luas Permukaan Balok
Diketahui sebuah balok memiliki ukuran panjang 10 cm, lebar 6 cm dan tinggi 5 cm. Berapa luas permukaan balok tersebut?
Penyelesaian:
L = 2 x (p x l + p x t + l x t)
L = 2 x (10 x 6 + 10 x 5 + 6 x 5)
L = 2 x (60 + 50 + 30)
L = 2 x 140
L = 280 cm²
Jadi, luas permukaan balok tersebut adalah 280 cm².
Rumus Keliling Balok
Keliling balok adalah jumlah seluruh panjang rusuk pada balok. Balok memiliki 12 rusuk yang terdiri dari 4 rusuk panjang, 4 rusuk lebar dan 4 rusuk tinggi. Dengan begitu, keliling balok dapat dihitung dengan rumus sebagai berikut:
| Rumus Keliling Balok (K) = 4 (p + l + t) |
Keterangan:
K = keliling balok
p = panjang balok
l = lebar balok
t = tinggi balok
Contoh Soal: Cara Menghitung Keliling Balok
Sebuah balok memiliki ukuran panjang 10 cm, lebar 8 cm dan tinggi 5 cm. Berapa keliling balok tersebut?
Penyelesaian:
K = 4 (p + l + t)
K = 4 (10 + 8 + 6)
K = 4 x 24
K = 96 cm
Jadi, keliling balok adalah 96 cm.
Rumus Rusuk Balok
Berikut merupakan cara mencari rusuk panjang, rusuk lebar dan rusuk tinggi jika diketahui volume atau luas permukaan balok.
Rumus Mencari Panjang Balok Jika Diketahui Volumenya
Untuk mencari rusuk panjang balok yang telah diketahui volumenya adalah:
| p = V : (l x t) |
Contoh Soal:
Diketahui volume sebuah balok adalah 1.000 cm³. Jika lebar balok 10 cm dan tingginya adalah 5 cm, berapa panjang balok tersebut?
Penyelesaian:
p = V : (l x t)
p = 1.000 : (10 x 5)
p = 1.000 : 50
p = 20 cm
Jadi, rusuk panjang balok adalah 20 cm.
Rumus Mencari Panjang Balok Jika Diketahui Luas Permukaannya
Untuk mencari rusuk panjang balok yang telah diketahui luas permukaannya adalah:
| p = (L : 2 – l x t) : l + t |
Contoh Soal:
Sebuah balok memiliki luas permukaan 280 cm². Jika lebar balok 6 cm dan tingginya 5 cm, berapa panjang balok tersebut?
Penyelesaian:
p = (L : 2 – l x t) : l + t
p = (280 : 2 – 6 x 5) : 6 + 5
p = (140 – 30) : 11
p = 110 : 11
p = 10 cm
Jadi, rusuk panjang balok adalah 10 cm.
Rumus Mencari Lebar Balok Jika Diketahui Volumenya
Untuk mencari rusuk lebar balok yang telah diketahui volumenya adalah:
| l = V : (p x t) |
Contoh Soal:
Diketahui volume balok adalah 600 cm³. Jika panjang balok 12 cm dan tingginya 5 cm, berapa lebar balok tersebut?
Penyelesaian:
l = V : (p x t)
l = 600 : (12 x 5)
l = 600 : 60
l = 10 cm
Jadi, rusuk lebar balok adalah 10 cm.
Rumus Mencari Lebar Balok Jika Diketahui Luas Permukaannya
Untuk mencari rusuk lebar balok yang telah diketahui luas permukaannya adalah:
| l = (L : 2 – p x t) : p + t |
Contoh Soal:
Diketahui sebuah balok memiliki luas permukaan 800 cm². Jika panjang balok 20 cm dan tingginya 5 cm, berapa lebar balok tersebut?
Penyelesaian:
l = (L : 2 – p x t) : p + t
l = (800 : 2 – 20 x 5) : 20 + 5
l = (400 – 100) : 25
l = 300 : 25
l = 12 cm
Jadi, rusuk lebar balok adalah 12 cm.
Rumus Mencari Tinggi Balok Jika Diketahui Volumenya
Untuk mencari rusuk tinggi balok yang telah diketahui volumenya adalah:
| t = V : (p x l) |
Contoh Soal:
Diketahui volume balok adalah 1.200 cm³. Jika panjang balok 15 cm dan lebarnya 10 cm, berapa tinggi balok tersebut?
Penyelesaian:
t = V : (p x l)
t = 1.200 : (15 x 10)
t = 1.200 : 150
t = 8 cm
Jadi, rusuk tinggi balok adalah 8 cm.
Rumus Mencari Tinggi Balok Jika Diketahui Luas Permukaannya
Untuk mencari rusuk tinggi balok yang telah diketahui luas permukaannya adalah:
| t = (L : 2 – p x l) : p + l |
Contoh Soal:
Diketahui sebuah balok memiliki luas permukaan 600 cm². Jika panjang baok 15 cm dan lebarnya 10 cm, berapa tinggi balok tersebut?
Penyelesaian:
t = (L : 2 – p x l) : p + l
t = (600 : 2 – 15 x 10) : 15 + 10
t = (300 – 150) : 25
t = 150 : 25
t = 6 cm
Jadi, rusuk tinggi balok adalah 6 cm.
Demikianah pembahasan lengkap mengenai bangun ruang balok mulai dari pengertian, bagian, ciri, jaring, rumus balok dan contoh soal tentang balok beserta cara menghitungnya. Semoga bermanfaat.
Baca Lagi :