Macam-Macam Bangun Datar Dan Ciri-Cirinya

Macam-Macam Bangun Datar Dan Ciri-Cirinya – Bangun datar merupakan bangun dua dimensi. Bangun datar memiliki beberapa jenis. Setiap jenisnya memiliki ciri-ciri yang berbeda antara yang satu dengan lainnya. Pada artike ini akan dibahas tentang macam-macam bangun datar lengkap beserta ciri-cirinya.

Bangun datar adalah suatu bangun yang merupakan bagian dari bidang datar (rata) yang dibatasi oleh garis-garis lurus atau garis lengkung. Bangun datar memiliki panjang dan lebar, tetapi tidak memiliki ketebalan. Oleh sebab itu, bangun datar hanya memiliki luas dan keliling, tetapi tidak memiliki volume.

Dalam pelajaran matematika, terdapat 8 jenis bangun datar yang dipelajari. Setiap bangun datar tersebut memiliki nama, ciri-ciri, dan rumus perhitungan luas dan keliling yang berbeda-beda. Untuk lebih jelasnya, simak pembahasan berikut ini.

Macam-Macam Bangun Datar Dan Ciri-Cirinya

Terdapat 8 jenis bangun datar yang dipelajari pada pelajaran matematika, yaitu persegi, persegi panjang, segitiga, jajar genjang, belah ketupat, layang-layang, trapesium, dan lingkaran.

1. Bangun Datar Persegi

Persegi adalah jenis bangun datar yang mempunyai empat sisi yang sama panjang dan memiliki empat sudut berbentuk sudut siku-siku. Ciri-ciri persegi adalah:

Memiliki 4 sisi sama panjang
Memiliki 4 sudut berbentuk sudut siku-siku
Sisi yang berhadapan sama panjang dan sejajar
Memiliki 2 garis diagonal
Garis diagonalnya saling bertemu tegak lurus
Memiliki 4 simetri lipat
Memiliki 4 simetri putar

Rumus Persegi

Berikut merupakan rumus untuk menghitung luas dan keliling persegi.

Luas (L) = s × s

Keliling (K) = 4 × s

Contoh Soal

Diketahui sebuah persegi mempunyai ukuran sisi 10 cm. Hitunglah berapa luas dan keliling persegi tersebut!

Penyelesaian:
L = s × s
L = 10 × 10
L = 100 cm²
Jadi, luas persegi tersebut adalah 100 cm².

K = 4 × s
K = 4 × 10
K = 40 cm
Jadi, keliling persegi tersebut adalah 40 cm.

2. Bangun Datar Persegi Panjang

Persegi panjang adalah bangun datar yang mempunyai dua pasang sisi sejajar dan sama panjang, serta memiliki empat sudut yang berbentuk siku-siku. Ciri-ciri persegi panjang adalah:

Memiliki 4 sisi
Memiliki 4 sudut berbentuk sudut siku-siku
Sisi yang berhadapan sama panjang dan sejajar
Memliki dua garis diagonal sama panjang
Memiliki 2 simetri lipat
Memliki 2 simetri putar

Rumus Persegi Panjang

Berikut merupakan rumus untuk menghitung luas dan keliling persegi panjang.

Luas (L) = p × l

Keliling (K) = 2 × (p + l)

Contoh Soal

Diketahui sebuah persegi panjang mempunyai ukuran panjang 10 cm dan lebar 5 cm. Hitunglah berapa luas dan keliling persegi panjang tersebut!

Penyelesaian:
L = p × l
L = 10 × 5
L = 50 cm²
Jadi, luas persegi panjang tersebut adalah 50 cm².

K = 2 × (p + l)
K = 2 × (10 + 5)
K = 2 × 15
K = 30 cm
Jadi, keliling persegi panjang tersebut adalah 30 cm.

3. Bangun Datar Segitiga

Segitiga adalah bangun datar yang mempunyai tiga sisi dan memiliki tiga sudut. Jika seluruh besar sudut pada segitiga dijumlahkan, besarnya adalah 180º. Segitiga memiliki beberapa jenis. Berdasarkan besar sudutnya, segitiga dibedakan menjadi segitiga lancip, segitiga siku-siku, dan segitiga tumpul. Sedangkan berdasarkan panjang sisinya, segitiga dibedakan menjadi segitiga sama sisi, segitiga sama kaki, dan segitiga sembarang. Ciri-ciri segitiga adalah:

Memiliki 3 sisi
Memiliki 3 sudut
Jumlah ketiga sudutnya adalah 180º

Rumus Segitiga

Berikut merupakan rumus untuk menghitung lua dan keliling segitiga.

Luas (L) = 1/2 × a × t

Keliling (K) = s + s + s

Contoh Soal

Diketahui sebuah segitiga siku-siku mempunyai ukuran sisi alas 5 cm, sisi miring 13 cm, dan tinggi 12 cm. Hitunglah berapa luas dan keliling segitiga tersebut!

Penyelesaian:
L = 1/2 × a × t
L = 1/2 × 5 × 12
L = 1/2 × 60
L = 30 cm²
Jadi, luas segitiga tersebut adalah 30 cm².

K = s + s + s
K = 5 + 13 + 12
K = 30 cm
Jadi, keliling segitiga tersebut adalah 30 cm.

4. Bangun Datar Jajar Genjang

Jajar genjang adalah bangun datar yang mempunyai dua pasang sisi sama panjang dan sejajar, serta memiliki dua pasang sudut yang sama besar (pasangan sudut lancip dan pasangan sudut tumpul). Ciri-ciri jajar genjang adalah:

Memiliki 4 sisi
Memiliki 4 sudut
Memiliki dua pasang sisi sejajar dan sama panjang
Sudut-sudut yang berhadapan sama besar
Memiliki dua sudut tumpul dan dua sudut lancip
Memiliki dua garis diagonal yang tidak sama panjang
Tidak memiliki simetri lipat
Memiliki 2 simetri putar

Rumus Jajar Genjang

Berikut merupakan rumus untuk menghitung luas dan keliling persegi panjang.

Luas (L) = a × t

Keliling (K) = 2 × (a + b)

Contoh Soal

Diketahui sebuah jajar genjang mempunyai ukuran sisi alas 10 cm, sisi miring 5 cm, dan tinggi 8 cm. Hitunglah berapa luas dan keliling jajar genjang tersebut!

Penyelesaian:
L = a × t
L = 10 × 8
L = 80 cm²
Jadi, luas jajar genjang tersebut adalah 80 cm².

K = 2 × (sisi alas + sisi miring)
K = 2 × (10 + 5)
K = 2 × 15
K = 30 cm
Jadi, keliling jajar genjang tersebut adalah 30 cm.

5. Bangun Datar Belah Ketupat

Belah ketupat adalah bangun datar yang memiliki empat sisi sama panjang dan memiliki dua pasang sudut sama besar. Ciri-ciri belah ketupat adalah:

Memiliki 4 sisi sama panjang
Memiliki 4 sudut
Sudut-sudut yang berhadapan sama besar
Memiliki dua garis diagonal
Garis diagonalnya berpotongan tegak lurus
Memiliki 2 simetri lipat
Memiliki 2 simetri putar

Rumus Belah Ketupat

Berikut merupakan rumus untuk menghitung luas dan keliling belah ketupat.

Luas (L) = 1/2 × d1 × d2

Keliling (K) = s + s + s + s

Contoh Soal

Diketahui ukuran diagonal sebuah belah ketupat adalah 10 cm dan 24 cm. Sedangkan ukuran sisi miringnya adalah 13 cm. Hitunglah berapa luas dan keliling belah ketupat tersebut!

Penyelesaian:
L = 1/2 × d1 × d2
L = 1/2 × 10 × 24
L = 1/2 × 240
L = 120 cm²
Jadi, luas belah ketupat tersebut adalah 120 cm².

K = 4 × s
K = 4 × 13
K = 52 cm
Jadi, keliling belah ketupat tersebut adalah 52 cm.

6. Bangun Datar Layang-Layang

Layang-layang adalah bangun datar yang mempunyai dua pasang sisi sama panjang dan memiliki sepasang sudut yang berhadapan sama besar. Ciri-ciri layang-layang adalah:

Memiliki 4 sisi
Memiliki 4 sudut
Memiliki dua pasang sisi sama panjang
Memiliki sepasang sudut sama besar
Memiliki 2 garis diagonal
Garis diagonalnya berpotongan tegak lurus
Memiliki satu simetri lipat

Rumus Layang-Layang

Berikut merupakan rumus untuk menghitung luas dan keliling layang-layang.

Luas (L) = 1/2 × d1 × d2

Keliling (K) = s + s + s + s

Contoh Soal

Diketahui diagonal sebuah layang-layang adalah 24 cm dan 24 cm. Jika sisi miring bagian atas masing-masing 15 cm dan sisi miring bagian bawah masing-masing 20 cm. Hitunglah berapa luas dan keliling laynag-layang tersebut!

Penyelesaian:
L = 1/2 × 24 × 24
L = 1/2 × 24 × 24
L = 1/2 × 576
L = 288 cm²
Jadi, luas layang-layang tersebut adalah 288 cm².

K = s + s + s + s
K = 15 + 20 + 15 + 20
K = 70 cm
Jadi, keliling layang-layang tersebut adalah 70 cm.

7. Bangun Datar Trapesium

Trapesium adalah bangun datar yang memiliki empat buah sisi, yang terdiri dari dua buah sisi yang sejajar, tetapi tidak sama panjang dan dua buah sisi lainnya tidak sama panjang dan tidak sejajar. Trapesium dibedakan menjadi 3 jenis, yakni trapesium sama kaki, trapesium siku-siku, dan trapesium sembarang. Ciri-ciri trapesium adalah:

Memiliki 4 sisi
Memiliki 4 sudut
Memiliki sepasang sisi yang sejajar, tetapi tidak sama panjang
Sudut-sudut diantara sisi sejajar besarnya 180°

Rumus Trapesium

Berikut merupakan rumus untuk menghitung luas dan keliling trapesium.

Luas (L) = 1/2 × (a + b) × t

Keliling (K) = s + s + s + s

Contoh Soal

Diketahui panjang sisi sejajar sebuah trapesium masing-masing 10 cm dan 15 cm. Jika tinggi trapesium 12 cm dan sisi miringnya 13 cm, hitunglah berapa luas dan keliling trapesium tersebut!

Penyelesaian:
L = 1/2 × (sisi sejajar 1 + sisi sejajar 2) × t
L = 1/2 × (10 + 15) × 12
L = 1/2 × 25 × 12
L = 1/2 × 300
L = 150 cm²
Jadi, luas trapesium tersebut adalah 150 cm².

K = s + s + s + s
K = 10 + 15 + 12 + 13
K = 50 cm
Jadi, keliling trapesium tersebut adalah 50 cm.

8. Bangun Datar Lingkaran

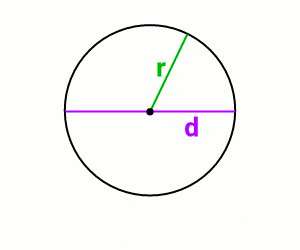
Lingkaran adalah bangun datar yang dibentuk oleh himpunan titik-titik yang mempunyai jarak sama dari suatu titik tetap (titik pusat). Ciri-ciri lingkaran adalah: