Jenis-Jenis Garis Dalam Matematika – Dalam pelajaran matematika kelas 4 SD, pasti telah diberikan materi tentang macam-macam garis. Untuk mengingat kembali apa saja nama macam-macam garis, berikut akan diberikan informasi mengenai jenis-jenis garis dalam matematika lengkap beserta gambarnya.
Garis adalah deretan titik-titik yang beraturan dan sejajar dengan jumlah tak terhingga. Kumpulan titik-titik tersebut saling terhubung antara yang satu dengan lainnya dan memanjang ke dua arah. Garis hanya memiliki satu dimensi, yaitu dimensi panjang.
Sebelum menyebutkan nama-nama jenis garis, kita perlu memahami apa saja istilah yang terdapat pada garis. berikut pembahasannya.
- Sinar, merupakan garis yang memiliki satu titik pangkal, sedangkan ujung lainnya dapat diteruskan ke segala arah yang tak hingga
- Segmen atau ruas garis, merupakan bagian dari sebuah garis yang dibatasi oleh dua titik akhir pada kedua ujungnya
- Garis vertikal, merupakan garis yang memiliki arah tegak berdiri
- Garis horizontal, merupakan garis yang memiliki arah lurus mendatar
Jenis-Jenis Garis Dalam Matematika Beserta Gambarnya
Dalam pembentukannya, setiap garis memiliki hubungan antara garis yang satu dengan lainnya. Hubungan antar garis akan membentuk garis baru yang merupakan dasar penamaan jenis garis. Berikut merupakan nama jenis-jenis garis dalam matematika beserta gambarnya masing-masing.
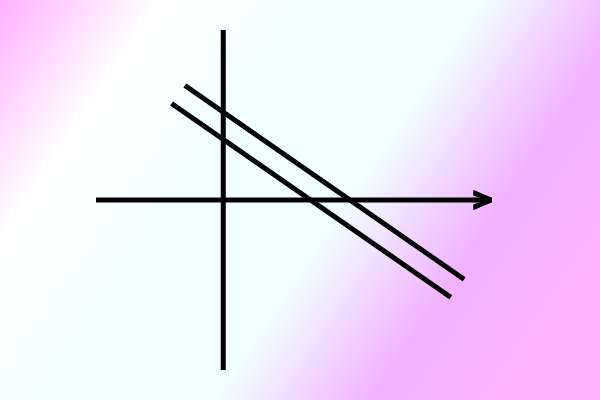
1. Garis Sejajar

Garis sejajar adalah dua garis atau lebih yang terletak pada bidang yang sama dan tidak berpotongan satu sama lain meskipun diperpanjang secara terus-menerus. Garis sejajar dinotasikan dengan simbol //. Pada gambar di atas, garis A sejajar dengan garis B, maka dapat dituliskan A // B.
Suatu garis dikatakan sejajar apabila memiliki sifat-sifat sebagai berikut:
- Jika terdapat suatu garis yang memotong salah satu dari dua garis sejajar, maka garis tersebut juga akan memotong garis lainnya
- Jika terdapat sebuah garis yang berkedudukan sejajar dengan dua buah garis, maka ketiga garis tersebut akan saling sejajar antara yang satu dengan yang lainnya
- Jika terdapat sebuah titik yang terletak di luar sebuah garis, maka terdapat satu garis yang sejajar dengan garis tersebut
2. Garis Berpotongan

Dua buah garis dikatakan saling berpotongan jika kedua garis tersebut terletak pada satu bidang datar dan berpotongan pada salah satu titiknya. Sehingga antara kedua garis memiliki sebuah titik potong atau titik persekutuan.
Perhatikan gambar diatas, garis F berpotongan dengan garis G di titik H. Adapun garis M yang berpotongan dengan garis N di titik O. Garis M dan N perpotongan membentuk sudut 90⁰, sehingga garis tersebut dinamakan garis berpotongan tegak lurus. Garis M dan N dan dapat dituliskan dengan simbol M 丄 N.
3. Garis Berimpit

Dua buah garis dikatakan berimpit apabila kedua garis tersebut saling menempel dan searah. Sehingga dapat dikatakan memiliki titik persekutuan yang tak terhingga. Garis yang berimpitan akan saling menutupi satu sama lain dan akan terlihat seperti satu garis lurus.
Sebagai contoh, dua garis yang berimpit dapat dilihat pada jarum jam yang menunjukan pukul 12.00, dimana jarum panjang dan jarum pendek saling berimpit dan yang terlihat hanya jarum panjangnya saja.
4. Garis Bersilangan

Dua buah garis dikatakan bersilangan apabila garis-garis tersebut tidak terletak pada satu bidang datar dan tidak akan berpotongan apabila diperpanjang.
Perhatikan garis AC dan garis HF pada gamabr kubus ABCD.EFGH. Terlihat bahwa kedua garis tersebut tidak terletak pada satu bidang datar. Garis AC terletak pada bidang ABCD, sedangkan garis HF terletak pada bidang EFGH. Apabila kedua garis tersebut diperpanjang, maka kedua garis tidak akan pernah bertemu dan tidak akan pernah berpotongan satu sama lain.
5. Garis Tegak Lurus

Dua buah garis dikatakan tegak lurus apabila memiliki kedudukan secara vertikal horizontal dan bertemu pada salah satu titiknya. Garis vertikal adalah yang memiliki arah tegak lurus, sedangkan garis horizontal adalah garis yang memiliki arah lurus mendatar.
Jika suatu garis yang berkedudukan secara vertikal dan horizontal berpotongan, maka akan membentuk garis tegak lurus dengan sudut 90⁰. Garis tegak lurus ini sering digunakan sebagai pertemuan untuk menggambarkan titik koordinat dalam matematika.
Demikianlah informasi mengenai jenis-jenis garis dalam matematika beserta gambar dan penjelasannya. Semoga bermanfaat.
Baca Lagi :