Rumus Luas Dan Keliling Segitiga Siku-Siku– Bangun segitiga memiliki beberapa jenis, diantaranya yaitu segitiga siku-siku. Pada kesempatan kali ini akan dibahas mengenai rumus luas dan keliling segitiga siku-siku beserta contoh soalnya.
Segitiga Siku-Siku
Segitiga siku-siku (rectangled triangle) adalah jenis segitiga yang salah satu sudutnya besarnya 90°. Segitiga siku-siku terbentuk dari dua buah sisi yang saling tegak lurus dan sisi lainnya yang disebut dengan sisi miring (hypotenusa).
Pada segitiga siku-siku, sisi miring merupakan sisi yang memiliki ukuran terpanjang. Sedangkan kedua sisi lainnya disebut dengan sisi alas dan sisi tinggi (tegak).
Perlu diketahui bahwa segitiga siku-siku mempunyai ciri-ciri yang berbeda dengan jenis segitiga lainya. Berikut merupakan sifat-sifat yang dimiliki oleh segitiga siku-siku:
- Mempunyai dua buah sisi yang saling tegak lurus
- Mempunyai satu buah sudut yangg berbentuk siku-siku
- Mempunyai satu buah sisi miring
- Memiliki satu simetri lipat
- Tidak memiliki simetri putar
Rumus Luas Dan Keliling Segitiga Siku-Siku
A. Rumus Luas Segitiga Siku Siku
Luas segitiga adalah ukuran seberapa besar daerah yang terletak di dalam sebuah segitiga yang dibatasi oleh sisi-sisi segitiga. Untuk menghitung luas segitiga siku-siku, kita harus mengetahui ukuran sisi alas dan tingginya. Jika sisi alas = a, dan tinggi = t, maka rumus luas segitiga siku-siku adalah sebagai berikut:
| Luas Segitiga Siku-Siku = 1/2 x a x t |
B. Rumus Keliling Segitiga Siku-Siku
Keliling segitiga adalah ukuran dari seluruh panjang sisinya. Untuk menghitung keliling segitiga siku-siku yaitu dengan menjumlahkan seluruh sisinya. Dengan begitu, rumus keliling segitiga siku-siku adalah:
| Keliling Segitiga Siku-Siku = sisi alas + sisi tegak + sisi miring |
C. Rumus Mencari Sisi Segitiga Siku-Siku
Untuk mencari salah satu ukuran sisi pada segitiga siku-siku, kita dapat menghitungnya dengan teorema pythagoras. Karena rumus pythagoras ini merupakan penjabaran sisi-sisi segitiga siku siku.
Teorema pythagoras atau yang sering disebut dengan teorema pythagoras merupakan hubungan antara sisi-sisi dalam segitiga siku-siku yang berbunyi:
| “Panjang sisi miring segitiga siku-siku sama dengan kuadrat panjang sisi lainnya.” |
Dari teorema pythagoras segitiga di atas, kita dapat menerapkannya untuk mencari sisi-sisi pada segitiga siku-siku. Jika sisi alas ditulis dengan huruf a, sisi tegak ditulis dengan huruf b, dan sisi miring ditulis dengan huruf c, maka rumus mencari sisi segitiga siku-siku adalah sebagai berikut:
1. Rumus Sisi Alas Segitiga Siku-Siku
| b² = c² – a² |
| b = √c² – a² |
2. Rumus Sisi Tinggi Segitiga Siku-Siku
| a² = c² – b² |
| a = √c² – b² |
3. Rumus Sisi Miring Segitiga Siku-Siku
| c² = a² + b² |
| c = √a² + b² |
Contoh Soal
1. Perhatikan gambar di bawah ini.
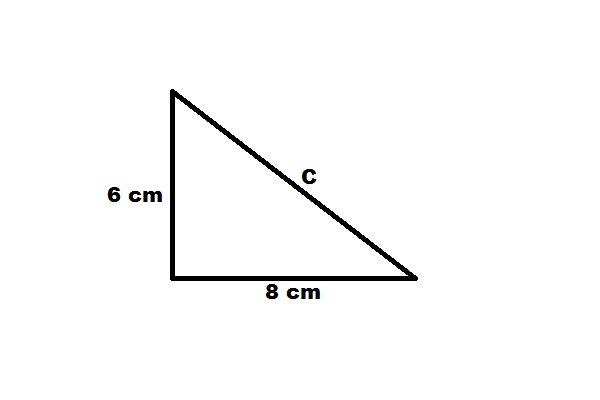
Hitunglah berapa panjang sisi miring (c) segitiga di atas!
Penyelesaian:
c² = a² + b²
c² = 6² + 8²
c² = 36 + 64
c² = 100
c = √100
c = 10 cm.
Jadi, panjang sisi miring c segitiga adalah 10 cm.
2. Sebuah segitiga siku-siku mempunyai panjang alas 12 cm dan tingginya 10 cm. Hitunglah berapa luas segitiga siku-siku tersebut!
Penyelesaian:
L = 1/2 x a x t
L = 1/2 x 12 x 10
L = 1/2 x 120
L = 60 cm².
Jadi, luas segitiga siku-siku adalah 60 cm².
3. Sebuah segitiga siku-siku mempunyai ukuran alas 24 cm, tinggi 7cm, dan sisi miringnya 25 cm. Hitunglah berapa keliling segitiga siku-siku tersebut!
Penyelesaian:
K = sisi1 + sisi2 + sisi3
K = 24 + 7 + 25
K = 56 cm.
Jadi, keliling segitiga siku-siku adalah 56 cm.
4. Ada sebuah benda berbentuk segitiga siku-siku dengan panjang alasnya 15 cm dan tinggi 20 cm. Berapakah luas benda tersebut !
Penyelesaian:
L = 1/2 x a x t
L = 1/2 x 15 x 20
L = 1/2 x 300
L = 150 cm².
Jadi, luas benda tersebut adalah 150 cm².
5. Sebuah segitiga siku-siku memiliki sisi miring 5 cm dan sisi tegak 4 cm. berapa panjang sisi alas segitiga siku-siku tersebut!
Penyelesaian:
a² = c² – b²
a² = 5² – 4²
a² = 25 – 16
a² = 9
a = √9
a = 3 cm.
Jadi, panjang alas segitiga siku-siku adalah 3 cm.
6. Sebuah segitiga siku-siku memiliki panjang alas 5 cm dan tinggi 12 cm. Hitunglah berapa luas dan keliling segitiga siku-siku tersebut!
Penyelesaian:
L = 1/2 x a x t
L = 1/2 x 5 x 12
L = 1/2 x 60
L = 30 cm².
Jadi, luas segitiga siku-siku adalah 30 cm².
Untuk menghitung keliling segitiga siku-siku, kita harus mencari sisi miringnya terlebih dahulu.
c² = a² + b²
c² = 5² + 12²
c² = 25 + 144
c² = 169
c = √169
c = 13 cm.
Keliling = sisi1 + sisi2 + sisi3
Keliling = 5 + 12 + 13
Keliling = 30 cm.
Jadi, keliling segitiga siku-siku adalah 30 cm.
Demikian pembahasan mengenai rumus luas dan keliling segitiga siku-siku beserta contoh soalnya. Semoga bermanfaat.
Baca Lagi :